$\LaTeX$基本语法
行间与行内公式
使用两个\$以创建一个行内公式:$123$
使用两个\$\$以创建行间公式:$$f(x)$$
p.s:若想在markdown中写出\$而不发生转义,应当在每个\$符号前加\,比如\\$
(这个\的数量有点玄学,你自己看着加吧)
转义与形式变换
| LaTeX | Symbol | LaTeX | Symbol |
|---|---|---|---|
| \# | $\#$ | \$ | $\$$ |
| \% | $\%$ | \{ | $\{$ |
| \backslash | $ \backslash$ | \& | $\&$ |
| \} | $\}$ | \_{i} | $_{i}$ |
| \vert | $\vert$ | \Vert | $\Vert$ |
| \langle | $\langle$ | \rangle | $\rangle$ |
| \lfloor | $\lfloor$ | \rfloor | $\rfloor$ |
| \lceil | $\lceil$ | \rceil | $\rceil$ |
| \llcorner | $\llcorner$ | \lrcorner | $\lrcorner$ |
| \ulcorner | $\ulcorner$ | \urcorner | $\urcorner$ |
| \uparrow | $\uparrow$ | \downarrow | $\downarrow$ |
| \Uparrow | $\Uparrow$ | \Downarrow | $\Downarrow$ |
| \alpha | $\alpha$ | \Alpha | $\Alpha$ |
| \beta | $\beta$ | \Beta | $\Beta$ |
| \gamma \digamma | $\gamma$ $\digamma$ | \Gamma \varGamma | $\Gamma$ $\varGamma$ |
| \delta | $\delta$ | \Delta \varDelta | $\Delta$ $\varDelta$ |
| \epsilon \varepsilon | $\epsilon$ $\varepsilon$ | \Epsilon | $\Epsilon$ |
| \zeta | $\zeta$ | \Zeta | $\Zeta$ |
| \theta \vartheta | $\theta$ $\vartheta$ | \Theta \varTheta | $\Theta$ $\varTheta$ |
| \iota | $\iota$ | \Iota | $\Iota$ |
| \kappa \varkappa | $\kappa$ $\varkappa$ | \Kappa | $\Kappa$ |
| \lambda | $\lambda$ | \Lambda \varLambda | $\Lambda$ $\varLambda$ |
| \mu | $\mu$ | \Mu | $\Mu$ |
| \sigma \varsigma | $\sigma$ $\varsigma$ | \Sigma \varSigma | $\Sigma$ $\varSigma$ |
| \omega | $\omega$ | \Omega \varOmega | $\Omega$ $\varOmega$ |
| \phi \varphi | $\phi$ $\varphi$ | \Phi \varPhi | $\Phi$ $\varPhi$ |
| \psi | $\psi$ | \Psi \varPsi | $\Psi$ $\varPsi$ |
| \chi | $\chi$ | \Chi | $\Chi$ |
| \pi \varpi | $\pi$ $\varpi$ | \Pi \varPi | $\Pi$ $\varPi$ |
| \eta | $\eta$ | \Eta | $\Eta$ |
| \rho \varrho | $\rho$ $\varrho$ | \Rho | $\Rho$ |
| \tau | $\tau$ | \Tau | $\Tau$ |
| \xi | $\xi$ | \Xi \varXi | $\Xi$ $\varXi$ |
| \upsilon | $\upsilon$ | \Upsilon \varUpsilon | $\Upsilon$ $\varUpsilon$ |
| \aleph | $\aleph$ | \beth | $\beth$ |
| \daleth | $\daleth$ | \gimel | $\gimel$ |
| \sum | $\sum$ | \prod | $\prod$ |
| \coprod | $\coprod$ | \biguplus | $\biguplus$ |
| \bigcap | $\bigcap$ | \bigcup | $\bigcup$ |
| \int | $\int$ | \oint | $\oint$ |
| \iint | $\iint$ | \oiint | $\oiint$ |
| \iiint | $\iiint$ | \oiiint | $\oiiint$ |
| \bigoplus | $\bigoplus$ | \bigotimes | $\bigotimes$ |
| \bigodot | $\bigodot$ | \bigvee | $\bigvee$ |
| \bigwedge | $\bigwedge$ | \bigsqcup | $\bigsqcup$ |
| \times | $\times$ | \cdot | $\cdot$ |
| \div | $\div$ | \pm | $\pm$ |
| \mp | $\mp$ | \ge | $\ge$ |
| \le | $\le$ | \gg | $\gg$ |
| \ll | $\ll$ | \ne | $\ne$ |
| \approx | $\approx$ | \equiv | $\equiv$ |
| \in | $\in$ | \notin | $\notin$ |
| \subseteq | $\subseteq$ | \subsetneqq | $\subsetneqq$ |
| \varnothing | $\varnothing$ | \emptyset | $\emptyset$ |
| \forall | $\forall$ | \exists | $\exists$ |
| \nexist | $\nexists$ | \emptyset | $\emptyset$ |
| \infty | $\infty$ | \partial | $\partial$ |
| \nabla | $\nabla$ | 1\degree | $1\degree$ |
| \propto | $\propto$ | 1^{^\circ} | $1^{^\circ}$ |
| \cicr | $\circ$ | \LaTeX | $\LaTeX$ |
标准函数名
| LaTeX | Symbol | LaTeX | Symbol |
|---|---|---|---|
| \sin | $\sin$ | \cos | $\cos$ |
| \tan | $\tan$ | \cot | $\cot$ |
| \sec | $\sec$ | \csc | $\csc$ |
| \arcsin | $\arcsin$ | \arccos | $\arccos$ |
| \arctan | $\arctan$ | ||
| \sinh | $\sinh$ | \cosh | $\cosh$ |
| \tanh | $\tanh$ | \coth | $\coth$ |
| \min | $\min$ | \max | $\max$ |
| \arg | $\arg$ | \deg | $\deg$ |
| \det | $\det$ | \dim | $\dim$ |
| \exp | $\exp$ | \hom | $\hom$ |
| \gcd | $\gcd$ | \ker | $\ker$ |
| \lg | $\lg$ | \ln | $\ln$ |
| \inf | $\inf$ | \sup | $\sup$ |
| \lim | $\lim$ | \liminf | $\liminf$ |
| \log | $\log$ | \limsup | $\limsup$ |
| \Pr | $\Pr$ |
| LaTeX | Symbol | LaTeX | Symbol |
|---|---|---|---|
| \~{i} | $~{i}$ | \^{i} | $^{i}$ |
| _i | $_i$ | ^i | $^i$ |
| \frac{a}{b} | $\frac{a}{b}$ | \dfrac{a}{b} | $\dfrac{a}{b}$ |
| \sqrt{n} | $\sqrt{n}$ | \sqrt[n]{a} | $\sqrt[n]{a}$ |
| \overline{n} | $\overline{n}$ | \underline{n} | $\underline{n}$ |
| \widehat{n} | $\widehat{n}$ | \widetilde{n} | $\widetilde{n}$ |
| \overrightarrow{n} | $\overrightarrow{n}$ | \underrightarrow{n} | $\underrightarrow{n}$ |
| \overleftarrow{n} | $\overleftarrow{n}$ | \underleftarrow{n} | $\underleftarrow{n}$ |
| \overbrace{abcde} | $\overbrace{abcde}$ | \underbrace{abcde} | $\underbrace{abcde}$ |
| 空格:~ | $a~s$ | \prod\limits_{i=0}^{n} | $\prod\limits_{i=0}^{n}$ |
| \max\limits_{{1\leq i\leq p}}\{ a_i \} | $\max\limits_{{1\leq i\leq p}}{ a_i }$ | \underset{x\in \mathbb{R}^n}{min} | $\underset{x\in \mathbb{R}^n}{min}$ |
| \varliminf\limits_{n\to\infty} | $\varliminf\limits_{n\to\infty}$ | \varlimsup\limits_{n\to\infty} | $\varlimsup\limits_{n\to\infty}$ |
| \xlongequal[subscript]{superscript} | $\xlongequal[subscript]{superscript}$ | \lim\limits_{x\to 0}\frac{x}{\sin x} | $\lim\limits_{x\to 0}\frac{x}{\sin x}$ |
| \left.\frac{\partial f}{\partial x}\right|_{x=0} | $\left.\frac{ \partial f}{ \partial x}\right|_{x=0}$ | \lim\limits_{x\to 0}\frac{x}{\sin x} | $\lim\limits_{x\to 0}\frac{x}{\sin x}$ |
$\mathbb{R}^3\backslash{0}$
我服了,抄不动了,这转义符是真的多,自己看图吧(水印懒得去了):
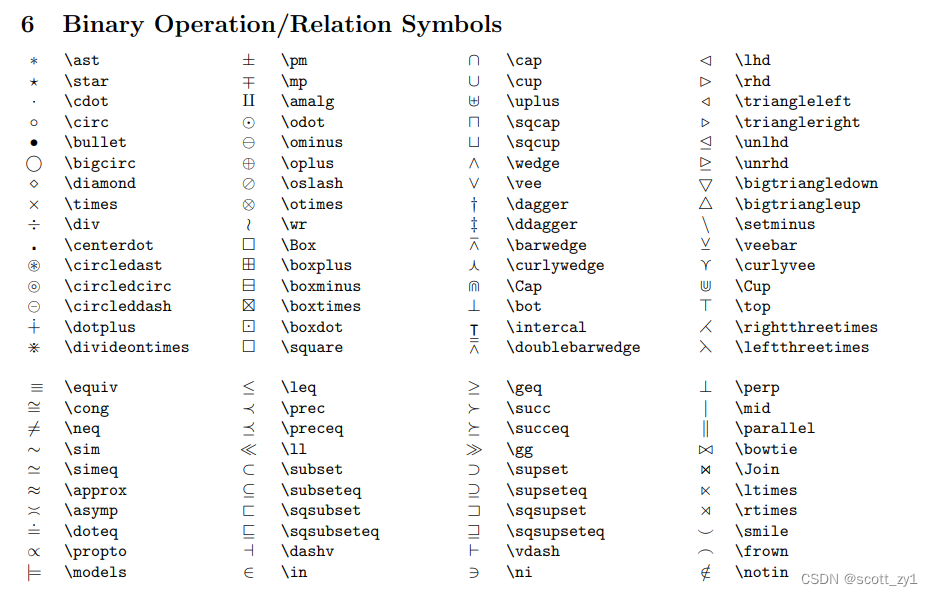




矩阵型
$\left(
\begin{array}{cc}
1 & 2 \\
3 & 4
\end{array}
\right)$
$\left( \begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right)$
$\left(
\begin{array}{cc}
1 & 2 \\
3 & 4
\end{array}
\right)
\left(
\begin{array}{c}
x \\
y
\end{array}
\right)$
$\left( \begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right)$
$\left[
\begin{array}{cc|c}
1 & 2 & 3 \\
4 & 5 & 6
\end{array}
\right]$
$\left[ \begin{array}{cc|c} 1 & 2 & 3 \\ 4 & 5 & 6 \end{array} \right]$
$f(x)=\left\{
\begin{array}{rcl}
1 & for & x>0 \\
0 & for & x=0 \\
-1 & for & x<0
\end{array}
\right.$
$f(x)=\left\{\begin{array}{rcl} 1 & for & x>0 \\ 0 & for & x=0 \\ -1 & for & x<0 \end{array}\right.$
一个快速生成表格的网站:tablesgenerator
多行公式
%自带编号单行公式
$\begin{equation}
a^2 + b^2 = c^2
\end{equation}$
$\begin{equation}
a^2 + b^2 = c^2
\end{equation}$
$\begin{equation} a^2 + b^2 = c^2 \end{equation}$ $\begin{equation} a^2 + b^2 = c^2 \end{equation}$
%带对其点的多行公式,对其&
%\nonumber用于取消标号
\begin{align}
a &= b + c \nonumber\\
d &= e + f \nonumber
\end{align}
$$\begin{align} a &= b + c-4 \nonumber\\ max(d) &= e + f \nonumber \end{align}$$
%居中对齐的多行公式
\begin{gather}
a = b + c \\
d = e + f
\end{gather}
$\begin{gather} a = b + c \\ max(d) = e + f \end{gather}$
关于颜色
单公式全局颜色:\color{颜色控制码}
单公式局部颜色:\textcolor{颜色控制码}{文本}
$\colorbox{orange}{单公式无框盒子:}$ \colorbox{文字背景颜色码}{文本}
$\fcolorbox{red}{magenta}{单公式盒子:}$ \fcolorbox{边框颜色码}{文字背景颜色码}{文本}
颜色控制码自定义:\color{#F4E040}{文字}
| 颜色控制码 | 颜色 |
|---|---|
| red | $\color{red}red$ |
| green | $\color{green}green$ |
| blue | $\color{blue}blue$ |
| pink | $\color{pink}pink$ |
| lightgreen | $\color{lightgreen}lightgreen$ |
| lightblue | $\color{lightblue}lightblue$ |
| orange | $\color{orange}orange$ |
| cyan | $\color{cyan}cyan$ |
| magenta | $\color{magenta}magenta$ |
| purple | $\color{purple}purple$ |
| brown | $\color{brown}brown$ |
| olive | $\color{olive}olive$ |
| lime | $\color{lime}lime$ |
| teal | $\color{teal}teal$ |
| violet | $\color{violet}voilet$ |
| black | $\color{black}black$ |
| gray | $\color{gray}gray$ |
| darkgray | $\color{darkgray}darkgray$ |
| lightgray | $\color{lightgray}lightgray$ |
| white | $\color{white}white$ |
| 颜色控制码 | 颜色 |
|---|---|
| maroon | $\color{maroon}maroon$ |
| crimson | $\color{crimson}crimson$ |
| orangered | $\color{orangered}orangered$ |
| coral | $\color{coral}coral$ |
| salmon | $\color{salmon}salmon$ |
| khaki | $\color{khaki}khaki$ |
| gold | $\color{gold}gold$ |
| goldenrod | $\color{goldenrod}goldenrod$ |
| tan | $\color{tan}tan$ |
| seagreen | $\color{seagreen}seagreen$ |
| forestgreen | $\color{forestgreen}forestgreen$ |
| yellowgreen | $\color{yellowgreen}yellowgreen$ |
| greenyellow | $\color{greenyellow}greenyellow$ |
| limegreen | $\color{limegreen}limegreen$ |
| springgreen | $\color{springgreen}springgreen$ |
| aquamarine | $\color{aquamarine}aquamarine$ |
| turquoise | $\color{turquoise}turquoise$ |
| cadetblue | $\color{cadetblue}cadetblue$ |
| skyblue | $\color{skyblue}skyblue$ |
| cornflowerblue | $\color{cornflowerblue}cornflowerblue$ |
| royalblue | $\color{royalblue}royalblue$ |
| midnightblue | $\color{midnightblue}midnightblue$ |
| navy | $\color{navy}navy$ |
| indigo | $\color{indigo}indigo$ |
| blueviolet | $\color{blueviolet}blueviolet$ |
| darkorchid | $\color{darkorchid}darkorchid$ |
| fuchsia | $\color{fuchsia}fuchsia$ |
| orchid | $\color{orchid}orchid$ |
| plum | $\color{plum}plum$ |
| linen | $\color{linen}linen$ |
| beige | $\color{beige}beige$ |
$\color{#c0ffee}{\LaTeX}$
关于字体
字体大小
$\displaystyle \int f^{n}(x-x_a)~dx $
$\textstyle \int f^{n}(x-x_a)~dx $
$\scriptstyle \int f^{n}(x-x_a)~dx $
$\scriptscriptstyle \int f^{n}(x-x_a)~dx $
$\displaystyle \int f^{n}(x-x_a)~dx $
$\textstyle \int f^{n}(x-x_a)~dx $
$\scriptstyle \int f^{n}(x-x_a)~dx $
$\scriptscriptstyle \int f^{n}(x-x_a)~dx $
$\Huge A$ $\huge B$ $\LARGE C$ $\Large D$ $\large E$ $\pmb F$ $\normalsize F$ $\small G$ $\footnotesize H$ $\scriptsize I$ $\tiny J$
$\Huge A$ $\huge B$ $\LARGE C$ $\Large D$ $\large E$ $\pmb F$ $\normalsize F$ $\small G$ $\footnotesize H$ $\scriptsize I$ $\tiny J$
字体
| LaTeX | Symbol | LaTeX | Symbol |
|---|---|---|---|
| \mathbb{R} | $\mathbb{R}$ | \mathsf{R} | $\mathsf{R}$ |
| \mathtt{R} | $\mathtt{R}$ | \mathit{R} | $\mathit{R}$ |
| \mathcal{R} | $\mathcal{R}$ | \mathrm{R} | $\mathrm{R}$ |
| \mathbf{R} | $\mathbf{R}$ | \mathop{R} | $\mathop{R}$ |
| \mathfrak{R} | $\mathfrak{R}$ | \mathscr{R} | $\mathscr{R}$ |
| \boldsymbol{R} | $\boldsymbol{R}$ |
$\mathbb{ABCDEFGHIJKLMNOPQRSTUVWXYZ}$ $\mathsf{ABCDEFGHIJKLMNOPQRSTUVWXYZ}$ $\mathtt{ABCDEFGHIJKLMNOPQRSTUVWXYZ}$ $\mathit{ABCDEFGHIJKLMNOPQRSTUVWXYZ}$ $\mathcal{ABCDEFGHIJKLMNOPQRSTUVWXYZ}$ $\mathrm{ABCDEFGHIJKLMNOPQRSTUVWXYZ}$ $\mathbf{ABCDEFGHIJKLMNOPQRSTUVWXYZ}$ $\mathop{ABCDEFGHIJKLMNOPQRSTUVWXYZ}$ $\mathscr{ABCDEFGHIJKLMNOPQRSTUVWXYZ}$ $\boldsymbol{ABCDEFGHIJKLMNOPQRSTUVWXYZ}$
附录
关于Markdown编辑LaTeX出现错误的解决
使用markdown编辑好blog再发布时,有时候会出现公式报错现象,比如
$\color{red}\rm Missing~or~unrecognized~delimiter~for ~\backslash left$
$\color{red}\rm Misplaced~\backslash hdashline$
$\color{red}\rm Misplaced~\backslash hline$
出现Missing or unrecognized delimiter for \left,Misplaced \hdashline和Misplaced \hline的原因一般是因为在markdown文件转html时用掉了LaTeX的\转义,导致实际在网页浏览LaTeX时,因为\的缺失出现公式报错。
解决方法非常简单,只需要在原LaTeX公式上的\处再加一个\即可,比如\\\。这样处理后就不用担心markdown转html时把\全转义完了。(如果原公式处是\\\,也应改为\\\\\\\)
一些规范
不能使用$sin(x)$
应当使用标准化的函数名$\sin(x)$
$sin(x)$
$\sin(x)$
英文字母只有在表示变量(或单一字符的函数名称)时才使用斜体,其余情况(如输入输出,常量)都应该使用罗马体(直立体)
$\rm ij$ \rm是范围变罗马体
$\text ij$ \text是单字符变罗马体
可使用$\text{ij}$扩展/限定范围
$x_i$,$i$表示变量$i=0,1,…$
$x_{\rm i}$,$\rm i$表示$\rm input$
一些例子
$\def\mathbi#1{\textbf{#1}}$
$\mathbi{A}$
$\def\mathbi#1{\textbf{#1}}$ $\mathbi{A}$
$\mathbb{R}^3\backslash\{0\}$
$\mathbb{R}^3\backslash{0}$
$f(x)=\frac 1 {\sqrt {2\pi} \sigma }{\rm e}^{-\frac {(x-\mu)}{2\sigma^2}}$
$f(x)=\frac 1 {\sqrt {2\pi} \sigma }{\rm e}^{-\frac {(x-\mu)}{2\sigma^2}}$
$$\sum_{n=1}^\infty \frac{1}{n^2} \to
\textstyle \sum_{n=1}^\infty \frac{1}{n^2} \to
\displaystyle \sum_{n=1}^\infty \frac{1}{n^2}$$
$$\sum_{n=1}^\infty \frac{1}{n^2} \to \textstyle \sum_{n=1}^\infty \frac{1}{n^2} \to \displaystyle \sum_{n=1}^\infty \frac{1}{n^2}$$
Compare $\displaystyle \lim_{t \to 0} \int_t^1 f(t)\, dt$
versus $\lim_{t \to 0} \int_t^1 f(t)\, dt$.
Compare $\displaystyle \lim_{t \to 0} \int_t^1 f(t), dt$ versus $\lim_{t \to 0} \int_t^1 f(t), dt$.
$\underset{j=1}{\overset{\infty}{\LARGE\mathrm K}}
\frac{a_j}{b_j}=
\cfrac{a_1}{
b_1+\cfrac{a_2}{
b_2+\cfrac{a_3}{
b_3+\ddots}
}
}
$
$\underset{j=1}{\overset{\infty}{\LARGE\mathrm K}}\frac{a_j}{b_j}=\cfrac{a_1}{b_1+\cfrac{a_2}{b_2+\cfrac{a_3}{b_3+\ddots}}}$
$$
f\left(
\left[
\frac{
1+\left\{x,y\right\}
}{
\left(
\frac{x}{y}+\frac{y}{x}
\right)
\left(u+1\right)
}+a
\right]^{3/2}
\right)
$$
$$ f\left( \left[ \frac{ 1+\left\{x,y\right\} }{ \left( \frac{x}{y}+\frac{y}{x} \right) \left(u+1\right) }+a \right]^{3/2} \right) $$
$$
\begin{aligned}
a=&\left(1+2+3+ \cdots \right. \\
& \cdots+ \left. \infty-2+\infty-1+\infty\right)
\end{aligned}
$$
$$ \begin{aligned} a=&\left(1+2+3+ \cdots \right. \\ & \cdots+ \left. \infty-2+\infty-1+\infty\right) \end{aligned} $$
$ cost(\theta)=\begin{equation}
\left\{
\begin{array}{lr}
-log(h_\theta(x))&y =1 \\
-log(1-h_\theta(x))&y=0
\end{array}
\right.
\end{equation}$
$ cost(\theta)=\begin{equation} \left\{ \begin{array}{lr} -log(h_\theta(x))&y =1 \\ -log(1-h_\theta(x))&y=0 \end{array} \right. \end{equation}$
$$
\left\langle
q
\middle\|
\frac{\frac{x}{y}}{\frac{u}{v}}
\middle|
p
\right\rangle
$$
$$
\left\langle
q
\middle|
\frac{\frac{x}{y}}{\frac{u}{v}}
\middle|
p
\right\rangle
$$
$$\Bigg(\bigg(\Big(\big((x)\big)\Big)\bigg)\Bigg)$$
$$\Bigg(\bigg(\Big(\big((x)\big)\Big)\bigg)\Bigg)$$
$$\begin{array}{c|rrrr}
& x^3 & x^2 & x^1 & x^0\\
& 1 & -6 & 11 & -6\\
{\color{red}1} & \downarrow & 1 & -5 & 6\\
\hline & 1 & -5 & 6 & |\phantom{-} {\color{blue}0}
\end{array}
$$
$$\begin{array}{c|rrrr}& x^3 & x^2 & x^1 & x^0\\ & 1 & -6 & 11 & -6\\ {\color{red}1} & \downarrow & 1 & -5 & 6\\ \hline & 1 & -5 & 6 & |\phantom{-} {\color{blue}0} \end{array} $$
$$\begin{array}{rrrr|ll}
x^3 & -6x^2 & +11x & -6 & x-1 \\
-x^3 & +x^2 & & & x^2-5x+6 \\ \hline
& -5x^2 & +11x & -6 \\
& \phantom{-}5x^2 & -5x & & && \\ \hline
& & +6x & -6 \\
& & -6x & +6 \\ \hline
& & 0 & 0
\end{array}$$
$$\begin{array}{rrrr|ll} x^3 & -6x^2 & +11x & -6 & x-1 \\ -x^3 & +x^2 & & & x^2-5x+6 \\ \hline & -5x^2 & +11x & -6 \\ & \phantom{-}5x^2 & -5x & & && \\ \hline & & +6x & -6 \\ & & -6x & +6 \\ \hline & & 0 & 0 \end{array}$$
$$\begin{array}{rrrrrrr|rr}
& x_1 & x_2 & s_1 & s_2 & s_3 & w & & \text{ratio} \\ \hline
s_1 & 0 & 1 & 1 & 0 & 0 & 0 & 8 & - \\
w & 1^* & -1 & 0 & -1 & 0 & 1 & 4 & 4 \\
s_3 & 1 & 1 & 0 & 0 & 1 & 0 & 12 & 12 \\ \hdashline
& 1 & -1 & 0 & -1 & 0 & 0 & 4 & \\ \hline
s_1 & 0 & 1 & 1 & 0 & 0 & 0 & 8 & \\
x_1 & 1 & -1 & 0 & -1 & 0 & 1 & 4 & \\
s_3 & 0 & 2 & 0 & 2 & 1 & -1 & 8 & \\ \hdashline
& 0 & 0 & 0 & 0 & 0 & -1 & 0 &
\end{array}$$
$$\begin{array}{rrrrrrr|rr} & x_1 & x_2 & s_1 & s_2 & s_3 & w & & \text{ratio} \\ \hline s_1 & 0 & 1 & 1 & 0 & 0 & 0 & 8 & - \\ w & 1^* & -1 & 0 & -1 & 0 & 1 & 4 & 4 \\ s_3 & 1 & 1 & 0 & 0 & 1 & 0 & 12 & 12 \\ \hdashline & 1 & -1 & 0 & -1 & 0 & 0 & 4 & \\ \hline s_1 & 0 & 1 & 1 & 0 & 0 & 0 & 8 & \\ x_1 & 1 & -1 & 0 & -1 & 0 & 1 & 4 & \\ s_3 & 0 & 2 & 0 & 2 & 1 & -1 & 8 & \\ \hdashline & 0 & 0 & 0 & 0 & 0 & -1 & 0 & \end{array}$$
$\begin{array}{|c|c|}\hline
自变量/因变量& 标量y & 向量 y & 矩阵Y \\ \hline
标量x & \frac{\partial y}{\partial x} & \frac{\partial y}{\partial x}&\frac{\partial Y}{\partial x} \\ \hline
向量x & \frac{\partial y}{\partial x} & \frac{\partial y}{\partial x}&\frac{\partial Y}{\partial x} \\ \hline
矩阵X & \frac{\partial y}{\partial X} & \frac{\partial y}{\partial X}&\frac{\partial Y}{\partial X} \\ \hline
\end{array}$
$$\begin{array}{|c|c|}\hline 自变量/因变量 & 标量y& 向量 y&矩阵Y\\ \hline 标量x & \frac{\partial y}{\partial x} & \frac{\partial y}{\partial x}&\frac{\partial Y}{\partial x} \\ \hline 向量x & \frac{\partial y}{\partial x} & \frac{\partial y}{\partial x}&\frac{\partial Y}{\partial x} \\ \hline 矩阵X & \frac{\partial y}{\partial X} & \frac{\partial y}{\partial X}&\frac{\partial Y}{\partial X} \\ \hline \end{array}$$