ACM模版集（随缘更新中）
基础板子
极简模板
爬小样例（CF专用）
TestCase Fetcher
杂项（常用）
Sieve筛子
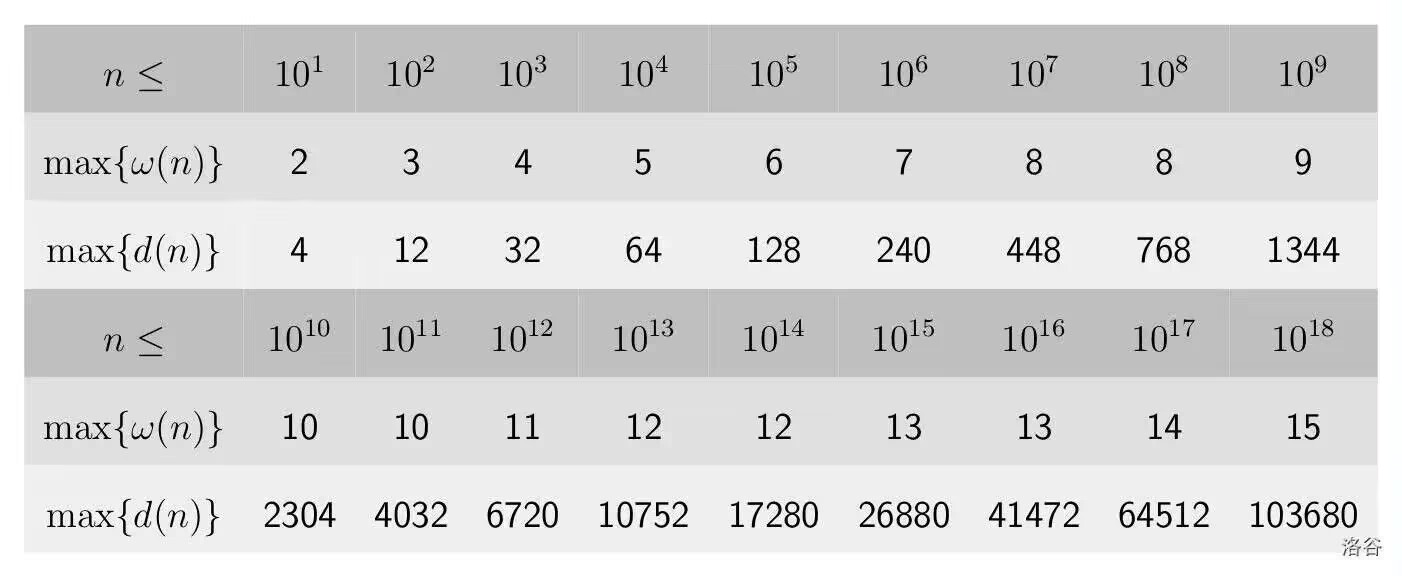
Sieve
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35struct Sieve {
std::vector<int> mpf; // minimum prime factor
std::vector<int> prime;
Sieve(int n) : mpf(n) {
for (int i = 2; i < n; i++) {
if (mpf[i] == 0) {
prime.push_back(i);
mpf[i] = i;
}
for (int j = 0; j < prime.size() and i * prime[j] < n; j++) {
mpf[i * prime[j]] = prime[j];
if (prime[j] == mpf[i])
break;
}
}
}
// get all factors
std::vector<int> getDiv(int x) const {
std::vector<int> _div(1, 1);
while (x > 1) {
int d = mpf[x];
int l = 0, r = _div.size();
while (x % d == 0) {
for (int k = l; k < r; k++) {
_div.push_back(_div[k] * d);
}
x /= d;
l = r, r = _div.size();
}
}
return _div;
}
};
快速幂
QuickPow
组合数预处理
Combination
随机数
Random
动态规划
01 / 完全背包
ZCbag
多重背包
Multibag
树形背包
ZCTBag
背包求方案数
ZCBagCnt
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25//求01/完全背包的，最优情况的方案数
i64 ZCBagCnt(int V, std::vector<int>& w, std::vector<int>& v) {//O(nV)
int n = w.size();
std::vector<i64> f(V + 1), g(V + 1);//求体积恰好等于j的最大价值；求体积恰好等于j的最大方案数
f[0] = 0;
g[0] = 1;
for (int i = 0; i < n; i++) {
for(int j = V;j >= w[i]; j--) {//01
//for(int j = w[i];j <= V; j++) {//完全
i64 cnt;
if (f[j] < f[j - w[i]] + v[i]) cnt = g[j - w[i]];
else if(f[j] == f[j - w[i]] + v[i]) cnt = g[j - w[i]] + g[j];
else cnt = g[j];
g[j] = cnt;//%mod;
f[j] = std::max(f[j], f[j - w[i]] + v[i]);
}
}
i64 res = 0;
for (int i = 0; i <= V; i++) res = std::max(res, f[i]);//找出最大价值
i64 cnt = 0;
for (int i = 0; i <= V; i++) //找出所有体积不同的最大价值，每个体积有不同的方案数，累加求和
if (f[i] == res) cnt += g[i];//%mod;
return cnt;
}
ZCBagCnt_V
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15//求01/完全背包的，体积恰好为V的方案数
i64 ZCBagCnt_V(int V, std::vector<int>& v) {//O(nV)
int n = v.size();
std::vector<i64> f(V + 1);
f[0] = 1;
for (int i = 0; i < n; i++) {
for (int j = V; j >= v[i]; j--) {//01
//for (int j = v[i]; j <= V; j++) {//完全
f[j] += f[j - v[i]];
}
}
return f[V];
}
ZBagCnt
背包求具体方案
ZbagSolve
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20//求01背包的最优具体方案
std::vector<int> ZbagSolve(int V, std::vector<int>& w, std::vector<int>& v) {
int n = w.size();
std::vector<std::vector<int>> f(n + 1, std::vector<int>(V + 1));
for(int i = n - 1; i >= 0; i--)
for(int j = 0; j <= V; j++) {
f[i][j] = f[i + 1][j];
if(j >= w[i]) f[i][j] = std::max(f[i][j], f[i + 1][j - w[i]] + v[i]);
}
std::vector<int> ans;
for(int i = 0, j = V; i < n; i++)
if(j >= w[i] && f[i][j] == f[i + 1][j - w[i]] + v[i]){
ans.push_back(i);
j -= w[i];
}
//最优情况的值是f[V]，懒得开for收集的时候再从这里传出去吧
return ans;
}
ZbagSolve
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29//求完全背包的最优具体方案
std::vector<int> CBagSolve(int V, std::vector<int>& w, std::vector<int>& v) {//O(nV)
int n = w.size();
std::vector<std::vector<int>> path(n + 1, std::vector<int>(V + 1));
std::vector<int> f(V + 1);
for (int i = 0; i < n; i++) {
for (int j = w[i]; j <= V; j++) {
path[i][j] = 0;
if (f[j] < f[j - w[i]] + v[i]) {
f[j] = f[j - w[i]] + v[i];
path[i][j] = 1;
}
}
}
std::vector<int> ans;
int i = n - 1;//N个物品
int j = V;//背包容量是V
while (i > 0 && j > 0) {
if (path[i][j] == 1) {
ans.push_back(i);
j -= w[i];
} else i--;
}
return ans;
}
最长上升子序列
LIS
最长不降子序列
LNDS
数据结构
树状数组
BIT(SIMPLE)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31template<typename T>
struct BIT {
std::vector<T> a;
int n;
BIT(int n_) {//下标从1开始
a.clear();
a.resize(n_ + 1);
n = n_;
}
BIT() {}
BIT(const BIT& bit) {//[可选] 复制bit（很少用）
n = bit.n;
a = bit.a;
}
T getsum(int x) {//获取[1, x]的和 O(logn)
T s = 0;
while (x) {
s += a[x];
x -= (x &- x);
}
return s;
}
void modify(int x, T val) {//单点增加x处的值 O(logn)
while (x <= n) {
a[x] += val;
x += (x &- x);
}
}
};
//附：想区间修改，区间查询的话，可以用这个维护差分数组（不过都只支持加减）
//区间推平，区间加乘，等操作，请换线段树
BIT(Capps)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35template <class T, class Merge = std::plus<T>>
struct BIT {//下标从1开始，到n结束
const Merge merge;
std::vector<T> t;
BIT(int n) : t(n + 1), merge(Merge()) {}
// O(n) build BIT
BIT(const std::vector<T> &a) : BIT(a.size()) {
int n = a.size();
for (int i = 1; i <= n; i++) {
t[i] = merge(t[i], a[i - 1]);
int j = i + (i & -i);
if (j <= n)
t[j] = merge(t[j], t[i]);
}
}
void modify(int i, const T &x) {
for (i += 1; i < t.size(); i += i & -i)
t[i] = merge(t[i], x);
}
T posQuery(int i) {//获取[1, i]的和 O(logn)
T res = T();
for (i += 1; i; i -= i & -i)
res = merge(res, t[i]);
return res;
}
// [可选，更换merge操作之后，得删掉] [l, r)
T rangeQuery(int l, int r) {
return posQuery(r - 1) - posQuery(l - 1);
}
};
rangeBIT(Capps)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36template <class T>
struct RangeBIT {//需要套个正常BIT板子
BIT<T> d, s;
RangeBIT(int n) : d(n), s(n) {}
// O(n) build RangeBIT
RangeBIT(std::vector<T> a)
: d(diff(a)), s(multIndex(diff(a))) {}
static std::vector<T> diff(std::vector<T> a) {
std::adjacent_difference(begin(a), end(a), begin(a));
return a;
}
static std::vector<T> multIndex(std::vector<T> a) {
for (int i = 0; i < a.size(); i++) {
a[i] *= i;
}
return a;
}
// [l, r)
void rangeModify(int l, int r, const T &x) {
d.modify(l, x), d.modify(r, -x);
s.modify(l, l * x), s.modify(r, -r * x);
}
// [l, r)
T rangeQuery(int l, int r) {
T res1 = r * d.posQuery(r - 1) - s.posQuery(r - 1);
T res2 = l * d.posQuery(l - 1) - s.posQuery(l - 1);
return res1 - res2;
}
};
//区间加，单点修改
MatBIT(Capps)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32template <class T, class Merge = std::plus<T>>
struct MatBIT {
const Merge merge;
std::vector<BIT<T, Merge>> t;
MatBIT(int n, int m)
: t(n + 1, BIT<T>(m)), merge(Merge()) {}
void modify(int x, int y, const T &v) {
for (int i = x + 1; i < t.size(); i += i & -i) {
t[i].modify(y, v);
}
}
T posQuery(int x, int y) {
T res = T();
for (int i = x + 1; i; i -= i & -i) {
res = merge(res, t[i].posQuery(y));
}
return res;
}
// [u, d), [l, r)
T rangeQuery(int u, int l, int d, int r) {
u -= 1, l -= 1, d -= 1, r -= 1;
T res1 = posQuery(d, r) + posQuery(u, l);
T res2 = posQuery(d, l) + posQuery(u, r);
return res1 - res2;
}
};
//二维树状数组，单点修改，区间查询
//或者维护二维差分：区间修改，单点查询
RangeMatBIT(Capps)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39template <class T>
struct RangeMatBIT {
MatBIT<T> p, px, py, pxy;
RangeMatBIT(int n, int m)
: p(n, m), px(n, m), py(n, m), pxy(n, m) {}
// [u, d), [l, r)
void rangeModify(int u, int l, int d, int r, const T &v) {
modify(u, l, v);
modify(d, r, v);
modify(u, r, -v);
modify(d, l, -v);
}
// [u, d), [l, r)
T rangeQuery(int u, int l, int d, int r) {
u -= 1, l -= 1, d -= 1, r -= 1;
return query(u, l) + query(d, r) - query(d, l) - query(u, r);
}
private:
void modify(int x, int y, const T &v) {
p.modify(x, y, v);
px.modify(x, y, v * x);
py.modify(x, y, v * y);
pxy.modify(x, y, v * x * y);
}
T query(int x, int y) {
T res = T();
res += p.posQuery(x, y) * (x + 1) * (y + 1);
res -= px.posQuery(x, y) * (y + 1);
res -= py.posQuery(x, y) * (x + 1);
res += pxy.posQuery(x, y);
return res;
}
};
//区间修改，区间查询
ST表
ST
线段树
单点修改，区间查询和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126//单点修改，区间查询。（可选功能：区间查找满足条件的第一个元素，区间查找满足条件的最后一个元素
template<class Info>// SGT template (from jiangly)
struct SGT {
int n;// size
std::vector<Info> info;// the info vector
SGT() : n(0) {}// default initialize
SGT(int n_, Info v_ = Info()) {// initialize with v
init(n_, v_);
}
template<class T>
SGT(std::vector<T> init_) {// initialize with a vector
init(init_);
}
void init(int n_, Info v_ = Info()) {// initialize with v
init(std::vector(n_, v_));
}
template<class T>
void init(std::vector<T> init_) {// initialize with a vector
n = init_.size();
info.assign(4 << std::__lg(n), Info());
std::function<void(int, int, int)> build = [&](int p, int l, int r) {
if (r - l == 1) {
info[p] = init_[l];
return;
}
int m = (l + r) / 2;
build(2 * p, l, m);
build(2 * p + 1, m, r);
pull(p);
};
build(1, 0, n);
}
void pull(int p) {// pull up the way of update
info[p] = info[2 * p] + info[2 * p + 1];
}
void modify(int p, int l, int r, int x, const Info &v) {// [original] SGT point modify
if (r - l == 1) {
info[p] = v;
return;
}
int m = (l + r) / 2;
if (x < m) {
modify(2 * p, l, m, x, v);
} else {
modify(2 * p + 1, m, r, x, v);
}
pull(p);
}
void modify(int p, const Info &v) {// [practice] SGT point modify
modify(1, 0, n, p, v);
}
Info rangeQuery(int p, int l, int r, int x, int y) {// [original] SGT range query
if (l >= y || r <= x) {
return Info();
}
if (l >= x && r <= y) {
return info[p];
}
int m = (l + r) / 2;
return rangeQuery(2 * p, l, m, x, y) + rangeQuery(2 * p + 1, m, r, x, y);// can be any other way of merge.[it is suggested to customize with operator overloaded, keeping this template as a black box]
}
Info rangeQuery(int l, int r) {// [practice] SGT range query
return rangeQuery(1, 0, n, l, r);
}
// [optional] you can ignore the following code if your don't want to use it when typing.
template<class F>
int findFirst(int p, int l, int r, int x, int y, F &&pred) {// [original] range find first
if (l >= y || r <= x) {
return -1;
}
if (l >= x && r <= y && !pred(info[p])) {
return -1;
}
if (r - l == 1) {
return l;
}
int m = (l + r) / 2;
int res = findFirst(2 * p, l, m, x, y, pred);
if (res == -1) {
res = findFirst(2 * p + 1, m, r, x, y, pred);
}
return res;
}
template<class F>
int findFirst(int l, int r, F &&pred) {// [practice] range find first
return findFirst(1, 0, n, l, r, pred);
}
template<class F>
int findLast(int p, int l, int r, int x, int y, F &&pred) {// [original] range find last
if (l >= y || r <= x) {
return -1;
}
if (l >= x && r <= y && !pred(info[p])) {
return -1;
}
if (r - l == 1) {
return l;
}
int m = (l + r) / 2;
int res = findLast(2 * p + 1, m, r, x, y, pred);
if (res == -1) {
res = findLast(2 * p, l, m, x, y, pred);
}
return res;
}
template<class F>
int findLast(int l, int r, F &&pred) {// [practice] range find last
return findLast(1, 0, n, l, r, pred);
}
};
// the way to use it:
// 1. create a struct to record the information you want
// 2. overload the operator "+" with this struct
// 3. declare your SGT with this struct and proper size
// *4. when using optional function, you should declare a lambda function to check if a particular information is vaild
struct Info {
int sum = 0;
};
Info operator+(const Info &a, const Info &b) {
return Info{(a.sum + b.sum) % m};
}
区间修改，区间查询
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
template<typename Info, typename Tag>
struct SGT {
#define lson (p<<1)
#define rson (p<<1|1)
std::vector<Info> ans;
std::vector<Tag> tag;
int n;
SGT() : n(0) {}
SGT(int n, Info v = Info()) {
init(std::vector<Info>(n, v));
}
SGT(std::vector<Info> a) {
init(a);
}
void init(std::vector<Info> a) {
n = a.size();
ans.resize(4 << std::__lg(n));
tag.resize(4 << std::__lg(n));
auto build = [&](auto&& self, int p, int l, int r) -> void {
if (r - l == 1) {
ans[p] = a[l];
return;
}
int m = (l + r) >> 1;
self(self, lson, l, m);
self(self, rson, m, r);
pushup(p);
};
build(build, 1, 0, n);
}
void pushup(int p) {
ans[p] = ans[lson] + ans[rson];
}
void pushdown(int p, int l, int r) {
int m = (l + r) / 2;
ans[lson] = ans[lson] + tag[p];
tag[lson] = tag[lson] + tag[p];
ans[rson] = ans[rson] + tag[p];
tag[rson] = tag[rson] + tag[p];
tag[p] = Tag();
}
void modify(int p, int l, int r, int x, int y, Tag k) {//区间修改
if (x <= l && r <= y) {
ans[p] = ans[p] + k;
tag[p] = tag[p] + k;
return;
}
pushdown(p, l, r);
int m = (l + r) >> 1;
if (x < m) modify(lson, l, m, x, y, k);
if (y > m) modify(rson, m, r, x, y, k);
pushup(p);
}
void modify(int l, int r, Tag k) {// [可选]
if (l == r) return;//
//assert(l < r && l >= 0 && r <= n);//可选
modify(1, 0, n, l, r, k);
}
Info query(int p, int l, int r, int x, int y) {//区间查询
if (x <= l && r <= y) return ans[p];
Info res;
pushdown(p, l, r);
int m = (l + r) >> 1;
if (x < m) res = res + query(lson, l, m, x, y);
if (y > m) res = res + query(rson, m, r, x, y);
return res;
}
Info query(int l, int r) { // [可选]
if (l == r) return Info();//
//assert(l < r && l >= 0 && r <= n);//可选
return query(1, 0, n, l, r);
}
#undef lson
#undef rson
void show() {
std::cout << "=======================\n";
for (int i = 0; i < n; i++) {
std::cout << query(i, i + 1).v << " ";
}
std::cout << "\n";
}
};
struct Info {//信息
int v;
Info(int v = 0) : v(v) {}
Info operator+(const Info& b) const {//信息直接合并方式
return Info(v | b.v);
}
};
struct Tag {//Tag信息
int v = -1;
Tag(int v = -1) : v(v) {}
Tag operator+(const Tag& b) const {//Tag之间合并关系
if (b.v == -1) return Tag(v);
return b;
}
};
//Tag与Info之间的合并关系
Info operator+(const Info& a, const Tag& b) {//赋值型Tag
//如果tag是某个非法值，那么不进行赋值操作
//否则进行赋值操作
if (b.v == -1) return a;
return Info(b.v);
}
//如果是区间加，Info里还需要维护区间长度
可持久化线段树
可持久化线段树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89template<typename T>
struct SGT_maintain {//可持久化线段树，单点修改，单点历史查询
struct node {int l, r; T v;};
int n;
std::vector<node> t;
std::vector<T> a;//下标从1开始
int num = 0;
std::vector<int> root;//保存历史版本编号
SGT_maintain(int n_) : n(n_), t(50 * n_), a(n_ + 1) {}
//k ： 版本编号
int build(int k, int l, int r) {//建树，先把a数组读完再build(0, 1, n);
num++;
k = num;
if (l == r) {
t[k].v = a[l];
return k;
}
int mid = (l + r) >> 1;
t[k].l = build(t[k].l, l, mid);
t[k].r = build(t[k].l, mid + 1, r);
return k;
}
void build() {// [可选]
save(build(0, 1, n));
}
void save(int k) {//新建备份
root.push_back(k);
}
int update(int k, int l, int r, int p, int v) {
num++;
t[num] = t[k];
k = num;
if (l == r) {
t[k].v = v;
} else {
int mid = (l + r) >> 1;
if (p <= mid) t[k].l = update(t[k].l, l, mid, p, v);
else t[k].r = update(t[k].r, mid + 1, r, p, v);
}
return k;
}
void update(int k, int p, int v) {// [可选]单点修改，同时更新历史版本
save(update(root[k], 1, n, p, v));
}
T query(int k, int l, int r, int p) {
if (l == r) {
return t[k].v;
}
int mid = (l + r) >> 1;
if (p <= mid) return query(t[k].l, l, mid, p);
else return query(t[k].r, mid + 1, r, p);
}
T query(int k, int p) {// [可选]单点历史版本查询
return query(root[k], 1, n, p);
}
};
void solve() {//使用例
int n, m;
std::cin >> n >> m;
SGT_maintain<int> sgt(n);
for (int i = 1; i <= n; i++) {
std::cin >> sgt.a[i];
}
sgt.build();
for (int i = 1; i <= m; i++) {
int v, op, p;
std::cin >> v >> op >> p;
if (op == 1) {
int x;
std::cin >> x;
sgt.update(v, p, x);
} else {
std::cout << sgt.query(v, p) << "\n";
sgt.save(sgt.root[v]);
}
}
}
区间第k小
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95//原理是原数组离散化之后，以数组下标为版本，更新各个数出现次数
template<typename T>
struct SGT_kth_maintain {//可持久化权值线段树，单点修改，查询rank为k的数
struct node {int l, r; T v;};
int n;
std::vector<node> t;//开50倍
std::vector<T> a;//下标从1开始
int num = 0;
std::vector<int> root;//保存历史版本编号
SGT_kth_maintain(int n_) : n(n_), t(100 * n_ + 1), a(n_ + 1) {}
//k ： 版本编号
int build(int l, int r) {//建树，不需要读入，初始化版本就是全0
num++;
int k = num;
if (l == r) {
return k;
}
int mid = (l + r) >> 1;
t[k].l = build(l, mid);
t[k].r = build(mid + 1, r);
return k;
}
void build() {// [可选] 建树
save(build(1, n));
}
void save(int k) {//新建备份
root.push_back(k);
}
int update(int k, int l, int r, int p) {//单点修改，同时更新历史版本
num++;
int num_ = num;
t[num_] = t[k];
t[num_].v++;
//k = num;
if (l == r) {
return num_;
//t[k].v = v;
} else {
int mid = (l + r) >> 1;
if (p <= mid) t[num_].l = update(t[k].l, l, mid, p);
else t[num_].r = update(t[k].r, mid + 1, r, p);
}
return num_;
}
void update(int k, int p) {// [可选] 单点修改(元素计数更新)，同时更新历史版本
save(update(root[k - 1], 1, n, p));
}
T query(int k1, int k2, int l, int r, int p) {//区间历史版本查询有多少数比p小
if (l == r) {
return l;//t[k].v;
}
int cnt = t[t[k2].l].v - t[t[k1].l].v;
int mid = (l + r) >> 1;
if (cnt >= p) return query(t[k1].l, t[k2].l, l, mid, p);
else return query(t[k1].r, t[k2].r, mid + 1, r, p - cnt);
}
T query(int l, int r, int p) {// [可选] 单点历史版本查询
return query(root[l - 1], root[r], 1, n, p);
}
};
void solve() {
int n, m;
std::cin >> n >> m;
std::vector<int> a(n);
for (auto &i : a) std::cin >> i;
auto b = a;
std::sort(b.begin(), b.end());
b.erase(std::unique(b.begin(), b.end()), b.end());
int n_ = b.size();
SGT_kth_maintain<int> sgt(n_);
sgt.build();
for (int i = 1; i <= n; i++) {
sgt.update(i, std::lower_bound(b.begin(), b.end(), a[i - 1]) - b.begin() + 1);
}
for (int i = 1; i <= m; i++) {
int l, r, k;
std::cin >> l >> r >> k;
std::cout << b[sgt.query(l, r, k) - 1] << "\n";
}
}
珂朵莉树
当数据随机时，用于快速处理与 “区间推平” 有关的题。
珂朵莉树
FHQ Treap
快速求数在数组的前驱，后继，排名（第几大），以及数组中第k大的数。同时可随意添加元素。
FHQ Treap
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131const int N=100005;
struct Treap
{
const int INF;
int Root,cnt;
deque<int>del_list;
struct Node
{
int ch[2],v,rnd,siz;
}node[N];
int newNode(int x)//申请新节点
{
int tmp;
if(del_list.empty()) tmp=++cnt;
else tmp=del_list.front(),del_list.pop_front();
node[tmp].rnd=rand(),node[tmp].v=x,node[tmp].siz=1,node[tmp].ch[0]=node[tmp].ch[1]=0;
return tmp;
}
void update(int x)//更新信息
{
node[x].siz=node[node[x].ch[0]].siz+node[node[x].ch[1]].siz+1;
}
void vsplit(int pos,int v,int &x,int &y)//按权值分裂
{
if(!pos)
{
x=y=0;
return;
}
if(node[pos].v<=v) x=pos,vsplit(node[pos].ch[1],v,node[pos].ch[1],y);
else y=pos,vsplit(node[pos].ch[0],v,x,node[pos].ch[0]);
update(pos);
}
void ssplit(int pos,int k,int &x,int &y)//按size分裂
{
if(!pos)
{
x=y=0;
return;
}
if(k>node[node[pos].ch[0]].siz)
x=pos,ssplit(node[pos].ch[1],k-node[node[pos].ch[0]].siz-1,node[pos].ch[1],y);
else y=pos,ssplit(node[pos].ch[0],k,x,node[pos].ch[0]);
update(pos);
}
int merge(int x,int y)//合并
{
if(!x||!y) return x+y;
if(node[x].rnd<node[y].rnd)
{
node[x].ch[1]=merge(node[x].ch[1],y);
update(x);
return x;
}
node[y].ch[0]=merge(x,node[y].ch[0]);
update(y);
return y;
}
void insert(int v)//插入
{
int x,y;
vsplit(Root,v,x,y);
Root=merge(merge(x,newNode(v)),y);
}
void erase(int v)//删除
{
int x,y,z;
vsplit(Root,v,x,z);
vsplit(x,v-1,x,y);
del_list.push_back(y);
y=merge(node[y].ch[0],node[y].ch[1]);
Root=merge(merge(x,y),z);
}
int pre(int v)//前驱
{
int x,y,cur;
vsplit(Root,v-1,x,y);
cur=x;
while(node[cur].ch[1]) cur=node[cur].ch[1];
merge(x,y);
return node[cur].v;
}
int nxt(int v)//后继
{
int x,y,cur;
vsplit(Root,v,x,y);
cur=y;
while(node[cur].ch[0]) cur=node[cur].ch[0];
merge(x,y);
return node[cur].v;
}
int get_rank(int v)//查排名
{
int x,y,ans;
vsplit(Root,v-1,x,y);
ans=node[x].siz;
merge(x,y);
return ans;
}
int kth(int k)//查排名为k的数
{
++k;
int x,y,cur;
ssplit(Root,k,x,y);
cur=x;
while(node[cur].ch[1]) cur=node[cur].ch[1];
merge(x,y);
return node[cur].v;
}
Treap():INF(2147483647)//构造函数初始化
{
Root=cnt=0;
insert(-INF),insert(INF);
}
};
//使用例：
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
Treap T;//声明对象
int n,t,x;
cin>>n;
while(n--){
cin>>t>>x;
if(t==1)cout<<T.get_rank(x)<<ET;//排名
else if(t==2)cout<<T.kth(x)<<ET;//第x大的数
else if(t==3)cout<<T.pre(x)<<ET;//前驱
else if(t==4)cout<<T.nxt(x)<<ET;//后继
else T.insert(x);//插入
}
return 0;
}
莫队
莫队(空模版)
莫队(区间众数)
莫队(区间本质不同数的奇偶性)
线性基
为什么放到数据结构里？因为我觉得它很像数据结构
给定集合，维护子集元素异或和最大值，最小值，是否存在某个子集异或和为x，子集异或和第k大，子集异或和排名
LineBasis
并查集
极简并查集
1
2
3
4
5
6
7
8const int N=100005;
int F[N];
int find(int x){//查询，自带路径压缩
return x==F[x]?x:F[x]=find(F[x]);
}
void join(int x,int y){//合并集合
F[find(x)]=find(y);
}
并查集（常用）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
struct DSU {
std::vector<int> F;
DSU(int n) : F(n + 1) {
std::iota(F.begin(), F.end(), 0);
}
void find(int x) {
return F[x] == x ? F[x] : F[x] = find(F[x]);
}
bool join(int x, int y) {
bool ok = (find(x) == find(y));
F[find(x)] = find(y);
return !ok;
}
};
并查集（模板类）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23template<typename T>
struct DSU {
map<T, T> F;
DSU(){}
void reset() {
F.clear();
}//重置
void init(T x) {
mp[x] = x;
}//需要自己手动初始化
T find(T x) {//溯源
if (F[x] != x) {
F[x] = find(F[x]);
}
return F[x];
}
void join(T x, T y) {//合并集合
T Fx = find(x), Fy = find(y);
if (Fx != Fy) {
F[Fx] = Fy;
}
}
};
带权并查集
pbdsTree
pbdsTree
Safe Unordered_Map
Safe Unordered_Map
图论
Kruskal
Kruskal
kruskal重构树
用于求图中，两点间最短路径的最大值的最小值。
（在整个图联通的情况下，最终共有 2n - 1个节点，树根编号为2n - 2；
若存在不联通的情况，需要用并查集维护每个联通块的最大编号，
然后向 2n - 1 号节点连边，最后以 2n - 1 为树根跑 HLD）
kruskal(MST)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49struct DSU {
std::vector<int> F;
DSU(int n) : F(n) {
std::iota(F.begin(), F.end(), 0);
}
DSU(const DSU& dsu_) {
F = dsu_.F;
}
int find(int x) {
return F[x] == x ? F[x] : F[x] = find(F[x]);
}
bool join(int x, int y) {
int fx = find(x), fy = find(y);
bool ok = (fx == fy);
F[fx] = fy;
return !ok;
}
};
// kruskal重构树（不需要边权） 节点值 连通性
std::tuple<std::vector<std::vector<int>>, std::vector<int>, DSU>
EXkruskal(std::vector<std::array<int, 3>> edgs, int n) {
//最小生成树求的是路径中最小值的最大值
//最大生成树求的是路径中最大值的最小值
std::sort(edgs.begin(), edgs.end());
DSU dsu(2 * n);
int cnt = n;
std::vector<int> val(2 * n);// 节点值
std::vector<std::vector<int>> edg(2 * n);
for (auto &[w, u, v] : edgs) {
int fu = dsu.find(u);
int fv = dsu.find(v);
if (fu != fv) {
edg[fu].push_back(cnt);
edg[fv].push_back(cnt);
// edg[u].push_back(cnt);
// edg[v].push_back(cnt);
val[cnt] = w;
dsu.join(fu, cnt);
dsu.join(fv, cnt);
cnt++;
if (cnt == 2 * n - 1) break;
}
}
return {edg, val, dsu};
}
dijkstra
Dijkstra
SPFA
SPFA
floyd
floyd
最大流最小割
MaxFlow
树论
重链剖分
Heave-Light Decomposition
字符串
KMP
1
2
3
4
5
6
7
8
9
10
11auto kmp(const std::string &s) {
int n = s.size();
std::vector<int> link(n);
for (int i = 1, j = 0; i < n; i++) {
while (j and s[i] != s[j])
j = link[j - 1];
j += (s[i] == s[j]);
link[i] = j;
}
return link;
}
Manacher
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19//给定一个字符串，该算法可以在 $O(n)$ 的复杂度下处理出该字符串每点的最大回文半径。
vector<int> manacher(string s) {//返回的R数组每项减1才是答案
string t="#";
for(auto c:s){t+=c;t+='#';}
int n=t.size();
vector<int> r(n);
for(int i=0,j=0;i<n;i++){
if(2*j-i>=0&&j+r[j]>i)r[i]=min(r[2*j-i],j+r[j]-i);
while(i-r[i]>=0&&i+r[i]<n&&t[i-r[i]]==t[i+r[i]])r[i]+=1;
if(i+r[i]>j+r[j])j=i;
}
return r;
}
vector<int> PR;
inline bool PAL(int l,int r){//判回文串（原理：判以(l+r)/2为中心的回文半径是否为l到r的长度）
return PR[r+l-1]-1==(r-l+1);//为什么要减一，看看上面的马拉车开头部分
//注意，这里双等号表示所求目标回文串不能是任何其他回文串的中心
//改成>=的话，就可以略去以上条件
}
字符串单哈希 (来自Hireathsoul，可能有点慢，不知道是不是base取太大了)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21//给定一个字符串，O(n)预处理，O(1)下判断字符串子串相等的工具
mt19937_64 rnd((ull)time(0));//随机数
ll hshb[]={2663545921,1000000019,1000000033,1000000061,1000000069,1000000097};
struct HASH{//带前导无效字符，下标从1开始
int n;
std::vector<ll> hsh,H;
ll p,base;
HASH(const std::string &s):n(s.size()),hsh(n),H(n){
base=hshb[rnd()%6];//随机模数，防止被卡
p = 1234567891;
hsh[0] = 1;
for (int i = 1; i <= n - 1; ++i){
hsh[i] = hsh[i - 1] * base % p;
H[i] = (H[i - 1] * base % p + s[i]) % p;
}
}
ll query(int l, int r){
return (H[r] - H[l - 1] * hsh[r - l + 1] % p + p) % p;
}
};
字符串双哈希（来自GWTM）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29struct Shash{
const ll base[2]={29,31};
const ll hashmod[2]={(ll)1e9+9,998244353};
array<vector<ll>,2>hsh;
array<vector<ll>,2>pwMod;
void init(string S){//传入时不需要加前导空字符，会自动加，下标从1开始
int n=S.size();S=' '+S;
hsh[0].resize(n+1),hsh[1].resize(n+1);
pwMod[0].resize(n+1),pwMod[1].resize(n+1);
for(int i=0;i<2;++i){
pwMod[i][0]=1;
for (int j=1;j<=n;++j){
pwMod[i][j]=pwMod[i][j-1]*base[i]%hashmod[i];
hsh[i][j]=(hsh[i][j-1]*base[i]+S[j])%hashmod[i];
}
}
}
pair<ll,ll>get(int l,int r){
pair<ll,ll> ans;
ans.first=(hsh[0][r]-hsh[0][l-1]*pwMod[0][r-l+1])%hashmod[0];
ans.second=(hsh[1][r]-hsh[1][l-1]*pwMod[1][r-l+1])%hashmod[1];
ans.first=(ans.first+hashmod[0])%hashmod[0];
ans.second=(ans.second+hashmod[1])%hashmod[1];
return ans;
}
};
bool same(Shash &a,int la,int ra,Shash &b,int lb,int rb){//查询
return a.get(la,ra)==b.get(lb,rb);
}
字符串N哈希（来自Capps）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52template <int D, std::array<int, D> B, std::array<int, D> P>
struct StringHash {
std::vector<std::array<int, D>> h;
template <class T>
StringHash(const T &s) : h(s.size() + 1) {
for (int i = 0; i < s.size(); i++) {
for (int k = 0; k < D; k++) {
h[i + 1][k] = (1ll * h[i][k] * B[k] + s[i] + 1) % P[k];
}
}
}
// [l, r)
std::array<int, D> get(int l, int r) {
static std::vector<std::array<int, D>> spow(1);
if (r - l < 0)
throw -1;
if (spow.size() < r - l + 1) {
if (spow[0][0] == 0) {
spow[0].fill(1);
}
int n = spow.size();
spow.resize(r - l + 1);
for (int i = n; i < spow.size(); i++) {
for (int k = 0; k < D; k++) {
spow[i][k] = 1ll * spow[i - 1][k] * B[k] % P[k];
}
}
}
std::array<int, D> res = {};
for (int k = 0; k < D; k++) {
res[k] = h[r][k] - 1ll * h[l][k] * spow[r - l][k] % P[k];
res[k] += (res[k] < 0 ? P[k] : 0);
}
return res;
}
};
//基数, 模数
using Hash = StringHash<2, {133, 331}, {int(1e9 + 21), int(1e9 + 33)}>;
using Hash = StringHash<3, std::array<int, 3>{1'000'003, 19260817, 998244353}, std::array<int, 3>{int(1e9) + 9, int(1e9 + 21), int(1e9 + 33)}>;
/*
没有默认构造函数，使用时开指针：
Hash *hs;
hs = new Hash(s);
hs->get(l, r);
*/
zFunction
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16//O(1)查询字符串以各个下标为起始下标时，最大的前缀匹配长度，
auto zFunction(const std::string &s) {
int n = s.size();
std::vector<int> z(n);
for (int i = 1, l = 0, r = 0; i < n; i++) {
if (i < r)
z[i] = min(z[i - l], r - i);
while (i + z[i] < n and s[i + z[i]] == s[z[i]])
z[i]++;
if (i + z[i] > r)
l = i, r = i + z[i];
}
z[0]=n;
return z;
}
Trie
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42struct trie {
std::vector<std::array<int, 26>> next;
std::vector<bool> exist;
int cnt = 0;
std::string t;// [可选] 用于记录dfs的子串
trie(int type, int len) {//size大小应满足 ：n <= sum(|s|)
next.resize(len * type);
exist.resize(len * type);
t.resize(len);
}
void insert(const std::string& s) {
int p = 0;
for (int i = 0; i < s.size(); i++) {
int c = s[i] - 'a';
if (!next[p][c]) next[p][c] = ++cnt;
p = next[p][c];
}
exist[p] = 1;
}
bool find(const std::string& s) {
int p = 0;
for (int i = 0; i < s.size(); i++) {
int c = s[i] - 'a';
if (!next[p][c]) return 0;
p = next[p][c];
}
return exist[p];
}
void dfs(int now, int dep) {// [可选] 先序遍历所有字符串（初始参数：0, 0）
if (exist[now]) {
std::cout << t.substr(0, dep) << "\n";// [editable] 该字符串即为一次遍历结果，这里修改对其进行的操作
}
for (int i = 0; i < 26; i++) {
if (next[now][i]) {
t[dep] = 'a' + i;
dfs(next[now][i], dep + 1);
}
}
}
};
01Trie
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27struct trie01 {
std::vector<std::array<int, 2>> next;
std::vector<bool> exist;
int cnt = 0;
trie(int n) {//size大小应满足 ：n <= sum(|s|)
next.resize(n);
exist.resize(n);
}
void insert(const std::string& s) { // 插入字符串s,l为字符串s的长度
int p = 0;
for (int i = 0; i < s.size(); i++) {
int c = s[i] - '0'; //这里是把char型换成int型0~25储存起来
if (!next[p][c]) next[p][c] = ++cnt; // 如果没有，就添加结点
p = next[p][c];
}
exist[p] = 1;
}
bool find(const std::string& s) { // 查找字符串 //可根据具体情况返回bool/int型
int p = 0;
for (int i = 0; i < s.size(); i++) {
int c = s[i] - '0';
if (!next[p][c]) return 0;
p = next[p][c];
}
return exist[p];
}
};
可撤回01Trie
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
struct trie01 {
std::vector<std::array<int, 2>> next;
std::vector<bool> exist;
std::vector<int> count;
int cnt = 0;
trie01(int n) {//size大小应满足 ：n <= 字符串长度 * 字符串种类数
next.resize(n);
exist.resize(n);
count.resize(n);
}
void insert(const std::string& s) { // 插入字符串s,l为字符串s的长度
int p = 0;
for (int i = 0; i < s.size(); i++) {
int c = s[i] - '0'; //这里是把char型换成int型0~25储存起来
if (!next[p][c]) next[p][c] = ++cnt; // 如果没有，就添加结点
count[p]++;
p = next[p][c];
}
count[p]++;
//exist[p] = 1;
}
void erase(const std::string& s) {
int p = 0;
for (int i = 0; i < s.size(); i++) {
int c = s[i] - '0'; //这里是把char型换成int型0~25储存起来
//if (!next[p][c]) next[p][c] = ++cnt; // 如果没有，就添加结点
count[p]--;
p = next[p][c];
}
count[p]--;
}
std::string get(const std::string& s) {
int p = 0;
std::string ans(33, '0');
int w = 0;
for (int i = 0; i < s.size(); i++) {
int c = s[i] - '0';
if (!next[p][1 ^ c] || count[next[p][1 ^ c]] == 0) {//对向无
p = next[p][c];
ans[w++] = '0';
} else {//对向有
p = next[p][1 ^ c];
ans[w++] = '1';
}
}
return ans;
}
// bool find(const std::string& s) { // 查找字符串 //可根据具体情况返回bool/int型
// int p = 0;
// for (int i = 0; i < s.size(); i++) {
// int c = s[i] - '0';
// if (!next[p][c]) return 0;
// p = next[p][c];
// }
// return exist[p];
// }
};
数学
欧拉函数
$O(\sqrt{n})$ 求欧拉函数值
getPhi
1
2
3
4
5
6
7
8
9
10
11
12
13
i64 getPhi(i64 n) {
i64 ans = n;
for (i64 i = 2; i <= n / i; i++) {
if (!(n % i)) {
ans = ans / i * (i - 1);
while (!(n % i)) n /= i;
}
}
if (n > 1) ans = ans / n * (n - 1);
return ans;
}
Phi
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
struct Phi {
std::vector<int> prime, phi, isp;
Phi(int n) {
isp = std::vector<int>(n + 1, 1);
phi.resize(n + 1);
isp[0] = isp[1] = 0;
phi[1] = 1;
for (int i = 2; i <= n; i++) {
if (isp[i]) {
prime.push_back(i);
phi[i] = i - 1;
}
for (int j = 0; j < prime.size() && i * prime[j] <= n; j++) {
isp[i * prime[j]] = 0;
if (!(i % prime[j])) {
phi[i * prime[j]] = phi[i] * prime[j];
break;
}
phi[i * prime[j]] = phi[i] * (prime[j] - 1);
}
}
}
};
莫比乌斯函数
mu
归并排序
排序，求逆序数
Merge Sort
容斥定理
非常简单的概念，集合学过吧，$A\bigcup B\bigcup C=A+B+C-(A\bigcap B)-(B\bigcap C)-(A\bigcap C)+(A\bigcap B\bigcap C)$，差不多就是这样的原理。
常用位运算进行集合操作，下面给出的是利用容斥定理求n以内与n不互质的数的个数的算法。$O(2^n)$（$n$ 为质因数个数）
ll cnt=d.size();//分解质因数的结果，不含1
ll ans=0;
for(ll i=1;i<(1<<cnt);i++){//
ll mul=1,num=0;
FOR(j,0,cnt-1){//
if(i&(1<<j)){//
num++;mul*=d[j];
}
}
if(num&1)ans+=n/mul;//
else ans-=n/mul;//
}
整除分块
整除分块
矩阵快速幂
Matrix（方阵）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179int M = 1e9 + 7;
struct Matrix {//
std::vector<std::vector<i64>> A;
int n;
Matrix(int n_) {
A = std::vector<std::vector<i64>>(n_, std::vector<i64>(n_, 0));
n = n_;
}
Matrix(const Matrix& B) {
A = B.A;
n = B.n;
}
std::vector<i64>& operator[](const int& i) {
return A[i];
}
Matrix operator+(Matrix &B) {
Matrix C = *this;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
(C[i][j] += B[i][j]) %= M;
}
}
return C;
}
Matrix operator-(Matrix &B) {
Matrix C = *this;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
(C[i][j] += M - B[i][j]) %= M;
}
}
return C;
}
void operator+=(Matrix &B) {// [可选]
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
(A[i][j] += B[i][j]) %= M;
}
}
}
void operator-=(Matrix &B) {// [可选]
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
(A[i][j] += M - B[i][j]) %= M;
}
}
}
Matrix operator*(Matrix &B) {
Matrix C(n);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
(C[i][j] += 1ll * A[i][k] * B[k][j] % M) %= M;
}
}
}
return C;
}
void operator*=(Matrix &B) {// [可选]
*this = *this * B;
}
Matrix operator^(i64 m) {
Matrix C(n), B = *this;
for (int i = 0; i < n; i++) {
C[i][i] = 1;
}
while (m) {
if (m & 1) C *= B;
B *= B;
m >>= 1;
}
return C;
}
void operator^=(const i64& n) {// [可选]
*this = *this ^ n;
}
int det() {// [可选] 行列式求值 O(n^2logn + n^3)
Matrix C = *this;
int w = 1;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
while (C[i][i]) {
int div = C[j][i] / C[i][i];
for (int k = i; k < n; k++) {
C[j][k] = (C[j][k] - 1ll * div * C[i][k] % M + M) % M;
}
std::swap(C[i], C[j]);
w = -w;
}
std::swap(C[i], C[j]);
w = -w;
}
}
i64 ans = 1;
for (int i = 0; i < n; i++) {
(ans *= C[i][i]) %= M;
}
ans = (M + w * ans) % M;
return ans;
}
Matrix INV() {// [可选] 矩阵求逆 O(n^3)
//std::cout << *this << "====\n";
Matrix tmp = *this, I(n);
for (int i = 0; i < n; i++) {
I[i][i] = 1;
}
for (int i = 0; i < n; i++) {
if (tmp[i][i] == 0) {
bool ok = 0;
for (int j = i + 1; j < n; j++) {
if (tmp[j][i]) {
std::swap(tmp[i], tmp[j]);
std::swap(I[i], I[j]);
ok = 1;
break;
}
}
if (!ok) return Matrix(0);//不可逆则返回空矩阵
}
int v = inv(tmp[i][i]);
for (int j = 0; j < n; j++) {
(tmp[i][j] *= v) %= M;
(I[i][j] *= v) %= M;
}
for (int j = i + 1; j < n; j++) {
if (tmp[j][i]) {
int v = tmp[j][i];
for (int k = 0; k < n; k++) {
(tmp[j][k] += (M - tmp[i][k] * v % M) % M) %= M;
(I[j][k] += (M - I[i][k] * v % M) % M) %= M;
}
}
}
//std::cout << i << ": \n" << tmp << "++++\n" << I << "----\n";
}
for (int i = n - 1; i >= 1; i--) {
for (int j = i - 1; j >= 0; j--) {
if (tmp[j][i]) {
int v = tmp[j][i];
for (int k = 0; k < n; k++) {
(tmp[j][k] += (M - tmp[i][k] * v % M) % M) %= M;
(I[j][k] += (M - I[i][k] * v % M) % M) %= M;
}
}
}
}
//std::cout << tmp << "====\n";
//std::cout << I << "====\n";
return I;
}
friend std::ostream& operator<<(std::ostream& COUT, Matrix B) {// [可选]
int n = B.n;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
COUT << B[i][j] << " \n"[j == n - 1];
}
}
return COUT;
}
};
/*
//用法举例：
Matrix a(2,2);
a[0][0]=1;a[0][1]=1;
a[1][0]=1;a[1][1]=0;
cout<<(a^n)[0][1];//求斐波那契第n项（模M）
Matrix b({ {1,2,3},
{4,5,6} });
(b*(b.T())).print();//矩阵乘法
*/
NMatrix（更一般的矩阵乘法）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109template<typename T>
struct Matrix {
int n, m;
std::vector<std::vector<T>> a;
Matrix(int n_,int m_) {
n = n_;
m = m_;
a = std::vector<std::vector<T>>(n, std::vector<T>(m, 0));
}
Matrix(std::vector<std::vector<T>> tmp) {// [可选] 快速创建矩阵（为什么C++98用不了brace-init啊）
n = tmp.size();
m = tmp[0].size();
a = std::vector<std::vector<T>>(n, std::vector<T>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
a[i][j] = tmp[i][j];
}
}
}
std::vector<T>& operator[](int i) {//重载运算符
return a[i];
}
Matrix<T> operator*(Matrix<T>& b) {//矩阵求积
Matrix tmp(n, b.m);
for (int i = 0; i < n; i++) {
for (int j = 0; j < b.m; j++) {
for (int k = 0; k < m; k++) {
tmp[i][j] += a[i][k] * b[k][j];
tmp[i][j] %= M;
}
}
}
return tmp;
}
Matrix<T> operator^(T n) {//快速幂
Matrix a = *this, ans = a;
ans = 1;//要用到单位矩阵的重载
while (n) {
if(n & 1) ans = ans * a;
a = a * a;
n >>= 1;
}
return ans;
}
void operator=(T n) {// [可选] 单位矩阵
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
a[i][j] = (i == j) * n;
}
}
}
//====接下来是一些和快速幂无关的函数
Matrix<T> RT() {// [可选] 矩阵求转置
Matrix tmp(m, n);
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
tmp[j][i] = a[i][j];
}
}
return tmp;
}
// std::vector<T> GuassElim() {//高斯消元求解线性方程组（取模意义下）,不会改变原矩阵
// auto b = *this;//复制一份
// assert(n == m - 1);//要求 列数比行数多一
// std::vector<T> tmp(m);//保存当前行
// for (int i = 0; i < n - 1; i++) {//用第几行开始向下消
// for (int j = 0; j < m; j++) {//预处理当前行
// if (b[i][m - 1 - i] == 0) {
// return std::vector<T>(m, -1);//无解
// }
// if (j != m - 1 - i) (b[i][j] *= inv(b[i][m - 1 - i])) %= M;//乘尾项逆元，归一化
// b[i][m - 1 - i] = 1;
// }
// for (int j = i + 1; i < n; i++) {//从之后的行开始消
// tmp = a[i];//复制
// for (int j = 0; j < m; j++) {//预处理当前行
// if (j != m - 1 - i) (b[i][j] *= inv(b[i][m - 1 - i])) %= M;//乘尾项逆元，归一化
// b[i][m - 1 - i] = 1;
// }
//准备开工
// //for ()
// }
// }
// }
void print(){//测试输出用，可以不写
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
std::cout << a[i][j] << " \n"[j == m - 1];
}
}
}
};
/*
//用法举例：
Matrix a(2,2);
a[0][0]=1;a[0][1]=1;
a[1][0]=1;a[1][1]=0;
cout<<(a^n)[0][1];//求斐波那契第n项（模M）
Matrix b({ {1,2,3},
{4,5,6} });
(b*(b.T())).print();//矩阵乘法
*/
gcd
求两数间最大公约数 $\gcd(x,y)$
ll gcd(ll a, ll b){
if(b == 0)return a;
return gcd(b, a % b);
}
//当然你也可以直接#include<algorithm>，然后用：
__gcd(x,y);
exgcd，扩展欧几里得
先了解裴蜀(贝祖)定理
裴蜀(贝祖)定理：若 $a,b$ 是整数,且 $\gcd(a,b)=d$，那么对于任意的整数 $x$、$y$，$ax+by$ 都一定是 $d$ 的倍数，特别地，一定存在整数 $x,y$，使 $ax+by=d$ 成立。 同时可知对于一般方程 $ax+by=c$ 有解的条件为 $\color{#ff6666}{c\equiv0~(mod~\gcd(a,b))}$。
拓展gcd即是要求 $ax+by=\gcd(a,b)$ 中 $x$、$y$ 的整数解
设有 $ax+by=\gcd(a,b)$，显然，当 $b = 0$ 时，$\gcd(a,b) = a$，$x = 1$，$y = 任何数$。为了方便这里使 $y = 0$。 当 $b \ne 0$ 时
EXGCD
BGSG
求解高次同余方程
BSGS
1
2
3
4
5
6
7
8
9
10
11
12
13
14i64 BSGS(i64 a,i64 b,i64 m){//求解a^x = b mod m
unordered_map<i64, i64> mp;
i64 r = b * a % m, t = sqrt(m) + 1;
for(int B = 1; B <= t; B++){
mp[r] = B;
r = (r * a) % m;
}
i64 at = powp(a, t, m), l = at;
for(int A = 1; A <= t; A++){
if (mp[l]) return A * t - mp[l];
l = (l * at) % m;
}
return -1;
}
组合数学
$(n,m)=(n,n-m)$
$(n,m)=(n-1,m)+(n-1,m-1)$
$k(n,k)=n(n-1,k-1)$
$k^{\underline{i}}(n,k)=n^{\underline{i}}(n-i,k-i)$
$(n,m)(m,k)=(n,k)(n-k,m-k)$
$\sum_{k=0}^n (m1,k)(m2,n-k)=(m1+m2,n)$
$\sum_{k=0}^n(k,m1)(n-k,m2)=(n+1,m1+m2+1)$
$\sum_{\sum B_i=M} \Pi _{i=1}^n (Bi,Ai) =(M+n-1,\sum Ai+n-1)$
$\sum_{i=0}^n (n,i)(i,j)=(n,j)*2^{n-j}$
$\sum_{i=0}^n(n,i)^2=(2n,n)$
$\sum_{i=0}^ni(n,i)=n2^{n-1}$
$\sum_{i=0}^ni^2(n,i)=n*(n+1)2^{n-2}$
$\sum_{i=0}^ni(n,i)^2=n*(2n-1,n-1)$
$\sum_{i=0}^k(i,k)=(n+1,k+1)$
$\sum_{i=0}^n(m+i,i)=(n+m+1,n)$
$\sum_{i=0}^n (m+i,s+i)=(n+m+1,n+s)$
$f_{n+1}= \sum_{i=0}^n(n-i,i) 其中f为斐波那契数列$
$\sum_{i=0}^n(n,i)x^{i}=(x+1)^n$
$\sum_{i=0}^n(n,i)a^{i}b^{n-i}=(a+b)^n$
$\ \sum_{i=0}^\infty (\alpha,i)x^{\alpha -i}y^i=(x+y)^{\alpha}$
$（\alpha,i）=\alpha^{\underline{i}} \setminus i!$
$\sum_{i=0}^m(-1)^i(n,i)=(-1)^m(n-1,m)$
允重组合：从n种数中，可重复地选m个数的方案总数： $H_n^m=C_{n - 1 + m}^{n - 1}$
Catalan数
$Catalan$ 数经常出现在组合计数的问题中，本质上和栈操作有关
下面直接放出 $Catalan$ 数的4个公式：
基本定义式：
$$CTL_n=\sum_{i=1}^{n}CTL_i\cdot CTL_{n-i}$$
递推式：
$$CTL_n=\frac{(4n-2)CTL_{n-1}}{n+1}$$
组合通项式：
$$CTL_n=\frac{\textrm{C}^n_{2n}}{n+1}$$
组合通项式2：
$$CTL_n=\textrm{C}^n_{2n}-\textrm{C}^{n-1}_{2n}$$
为什么要记这么多式子？当然是推式子化简需要。
计算几何
基本来自Capps
点（二维）
Point
有关线的操作
Point - Line
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31// a on Seg b-c
bool onSeg(Point a, Point b, Point c) {
b = b - a, c = c - a;
return b % c == 0 and b * c <= 0;
}
// a disTo Line b-c
ld disToLine(Point a, Point b, Point c) {
Point v1 = b - c, v2 = a - c;
return 1.L * std::abs(v1 % v2) / sqrtl(v1 * v1);
}
// a disTo Seg b-c
ld disToSeg(Point a, Point b, Point c) {
if ((a - b) * (c - b) <= 0 or (a - c) * (b - c) <= 0) {
return std::min(dis(a, b), dis(a, c));
}
return disToLine(a, b, c);
}
// a project to Line b-c (here Point = Point<ld, ld>)
Point foot(Point a, Point b, Point c) {
Point u = a - b, v = c - b;
return b + 1.L * (u * v) / (v * v) * v;
}
// a symmetry to Line b-c (here Point = Point<ld, ld>)
Point symmetry(Point a, Point b, Point c) {
Point ft = foot(a, b, c);
return 2 * ft - a;
}
Line - Line
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28// Line a-b cross Line c-d (here Point = Point<ld, ld>)
Point cross(Point a, Point b, Point c, Point d) {
Point v = c - d;
ld sa = v % (a - d), sb = (b - d) % v;
return 1.L * sa / (sa + sb) * (b - a) + a;
}
const ld pi = acosl(-1);
// a-b 和 a-c 的夹角 signed
ld getAngle(Point a, Point b, Point c) {
auto v1 = b - a, v2 = c - a;
return atan2l(v1 % v2, v1 * v2); // ∠bac
}
int sgn(const ld &a) {
return (a < -eps ? -1 : a > eps);
}
// 对四个不同的点判断四点共圆
// d在abc外接圆外return 1, 内return -1
int inCircle(Point a, Point b, Point c, Point d) {
ld ag1 = getAngle(a, b, c), ag2 = getAngle(d, c, b);
if (sgn(ag1) == sgn(ag2)) {
return sgn(PI - std::abs(ag1 + ag2));
} else {
return sgn(std::abs(ag1) - std::abs(ag2));
}
}
多边形
凸包
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29PS convex(PS ps) {
std::sort(ps.begin(), ps.end());
ps.erase(std::unique(ps.begin(), ps.end()), ps.end());
const int n = ps.size();
if (n <= 1) {
return ps;
}
PS hull(n + 1);
int k = -1;
for (int i = 0; i < n; i++) {
while (k >= 1 and (hull[k] - hull[k - 1]) % (ps[i] - hull[k]) <= 0) {
k -= 1;
}
hull[++k] = ps[i];
}
for (int i = n - 2, m = k + 1; i >= 0; i--) {
while (k >= m and (hull[k] - hull[k - 1]) % (ps[i] - hull[k]) <= 0) {
k -= 1;
}
hull[++k] = ps[i];
}
assert(k >= 2);
return hull.resize(k), hull;
}
求凸包面积
1
2
3
4
5
6
7
8ld area(const PS &ps) {
ld res = 0;
for (int i = 0; i < ps.size(); i++) {
int j = (i + 1) % ps.size();
res += ps[i] % ps[j];
}
return res / 2;
}
Point - Polygon
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54// #include "onSeg"
class InPoly {
// Seg c-d is Cross Seg a-b
bool isCross(Point a, Point b, Point c, Point d) const {
Vector ab = b - a, cd = d - c;
if (ab % cd == 0)
return 0; // 共线,寄
int r1 = sgn(ab % (c - a)), r2 = sgn(ab % (d - a));
int g1 = sgn(cd % (a - c)), g2 = sgn(cd % (b - c));
return !(r1 * r2 > 0 or r1 + r2 == -1 or g1 * g2 > 0);
// 真相交或者 c-d 贴着 a-b 左边
}
public:
// a IN/OUT/ON Polygon
std::string operator()(Point a, const PS &ps) const {
int res = 0;
Vector b = {1 << 30, a.y};
for (int i = 0; i < ps.size(); i++) {
int j = (i + 1) % ps.size();
if (onSeg(a, ps[i], ps[j]))
return "ON";
res += isCross(a, b, ps[i], ps[j]);
}
return (res % 2 ? "IN" : "OUT");
}
};
const InPoly inPoly;
// a IN/OUT/ON Convex
std::string inConvex(Point a, const PS &ps) {
if (a == ps[0])
return "ON";
if (ps.size() <= 1)
return "OUT";
if (ps.size() == 2)
return onSeg(a, ps[0], ps[1]) ? "ON" : "OUT";
auto v = a - ps[0];
if ((ps[1] - ps[0]) % v < 0 or (ps.back() - ps[0]) % v > 0)
return "OUT";
int l = 1, r = ps.size() - 1;
while (l + 1 < r) {
auto mid = l + r >> 1;
auto res = (ps[mid] - ps[0]) % v;
if (res == 0)
return (ps[mid] == a ? "ON" : (onSeg(a, ps[0], ps[mid]) ? "IN" : "OUT"));
(res > 0 ? l : r) = mid;
}
auto res = (ps[r] - ps[l]) % (a - ps[l]);
if (res == 0 or onSeg(a, ps[0], ps[l]) or onSeg(a, ps[0], ps[r]))
return "ON";
return (res > 0 ? "IN" : "OUT");
}
Line - Polygon
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34PS cutPoly(const PS &ps, Point a, Point b) {
// 返回多边形 ps 在有向直线 a->b 左边的部分
PS v;
auto c = b - a;
for (int i = 0; i < ps.size(); i++) {
int j = (i + 1) % ps.size();
auto cr1 = c % (ps[i] - a), cr2 = c % (ps[j] - a);
if (cr1 >= 0)
v.push_back(ps[i]);
if (sgn(cr1) * sgn(cr2) == -1)
v.push_back(cross(a, b, ps[i], ps[j]));
}
return v;
}
// find point of tangency
class BinarySearchOnConvex {
PS vs;
public:
constexpr BinarySearchOnConvex(const PS &ps) : vs(ps.size()) {
int n = size(ps);
for (int i = 0; i < n; i++) {
int j = (i + 1) % n;
vs[i] = ps[j] - ps[i];
}
}
int operator()(Point a) const {
int res = std::lower_bound(begin(vs), end(vs), a, polarCmp) - begin(vs);
return res % size(vs);
}
};
求两凸包闵可夫斯基和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28PS minkowski(const PS &a, const PS &b) {
int n = a.size(), m = b.size();
if (!n or !m)
return PS();
PS ps(1, a[0] + b[0]);
int ap = 0, bp = 0;
while (ap < n and bp < m) {
auto va = a[(ap + 1) % n] - a[ap];
auto vb = b[(bp + 1) % m] - b[bp];
auto res = va % vb;
if (res > 0)
ps.push_back(ps.back() + va), ap++;
if (res < 0)
ps.push_back(ps.back() + vb), bp++;
if (res == 0)
ps.push_back(ps.back() + va + vb), ap++, bp++;
}
while (ap < n) {
auto va = a[(ap + 1) % n] - a[ap];
ps.push_back(ps.back() + va), ap++;
}
while (bp < m) {
auto vb = b[(bp + 1) % m] - b[bp];
ps.push_back(ps.back() + vb), bp++;
}
return ps.pop_back(), ps;
}
一些具体应用
最小圆覆盖
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35//需要cross（在Line - Line里）
Point excir(const Point &a, const Point &b, const Point &c) {
// 三点求外接圆 圆心
auto d1 = 0.5 * (a + b), d2 = d1 + (a - b).rotate();
auto d3 = 0.5 * (c + b), d4 = d3 + (c - b).rotate();
return cross(d1, d2, d3, d4);
}
struct MinCircleOver {
pii Center;
ld Radius = 0;
MinCircleOver(PS ps) {//理论O(n^3)，但随机化之后，期望复杂度是O(n)
std::shuffle(begin(ps), end(ps), std::mt19937(time(0)));
for (int i = 0; i < ps.size(); i++) {
if (sgn(dis(Center, ps[i]) - Radius) <= 0)
continue;
// i点不在圆内,说明 i要更新圆
Center = ps[i], Radius = 0;
for (int j = 0; j < i; j++) {
if (sgn(dis(Center, ps[j]) - Radius) <= 0)
continue;
// j不在圆内,说明 j要更新圆
Center = 0.5f * (ps[i] + ps[j]), Radius = dis(Center, ps[i]);
for (int k = 0; k < j; k++) {
if (sgn(dis(Center, ps[k]) - Radius) <= 0)
continue;
// k不在圆内,说明 k要更新圆
Center = excir(ps[i], ps[j], ps[k]), Radius = dis(Center, ps[i]);
}
}
}
}
};
平面最近点对
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// 得到平面最近点对距离的平方
template <class T, class G>
G closestPair(std::vector<Point<T, G>> ps) {
auto pf = [&](const T &x) {
return 1ll * x * x;
};
G ans = 1ll << 60;
std::function<void(int, int)> find = [&](int l, int r) {
if (r - l <= 1)
return;
int mid = l + r >> 1;
find(l, mid), find(mid, r);
std::vector<Point<T, G>> b; // points in caught
for (int i = l; i < r; i++)
if (pf(std::fabs(ps[i].x - ps[mid].x)) < ans)
b.push_back(ps[i]);
std::sort(b.begin(), b.end(), [&](pii u, pii v) {
return u.y < v.y; // sort by y
});
for (int i = 0; i < b.size(); i++)
for (int j = i + 1; j < b.size() and pf(b[j].y - b[i].y) < ans; j++)
ans = std::min(ans, dis2(b[j] - b[i]));
};
std::sort(begin(ps), end(ps)); // sort by x
find(0, ps.size());
return ans;
}
// O(nlog2n) but almost O(nlogn)
三角剖分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197const ld pi = acosl(-1);
// a-b 和 a-c 的夹角 signed
ld getAngle(Point a, Point b, Point c) {
auto v1 = b - a, v2 = c - a;
return atan2l(v1 % v2, v1 * v2); // ∠bac
}
// 对四个不同的点判断四点共圆
// d在abc外接圆外return 1, 内return -1
int inCircle(Point a, Point b, Point c, Point d) {
auto ag1 = getAngle(a, b, c), ag2 = getAngle(d, c, b);
if (sgn(ag1) == sgn(ag2)) {
return sgn(pi - std::abs(ag1 + ag2));
} else {
return sgn(std::abs(ag1) - std::abs(ag2));
}
}
struct Delaunay {
struct Edge {
Edge *l, *r, *inv;
int face, from;
Edge() : face{0}, from{-1} {
l = r = inv = nullptr;
}
};
void addFace(Edge *e0, Edge *e1, Edge *e2, int fid) {
e0->r = e2->l = e1;
e1->r = e0->l = e2;
e2->r = e1->l = e0;
e0->face = e1->face = e2->face = fid;
face[fid] = e0;
}
void init() {
bucket.resize(2 * (n + 1));
vertex.resize(n + 3);
// 加三个点构造全局三角形
ps.emplace_back(Inf * 10, Inf);
ps.emplace_back(-Inf, Inf);
ps.emplace_back(-Inf, -Inf * 10);
std::vector<Edge *> e(6);
for (auto &pt : e) {
pt = new Edge();
}
e[0]->from = e[5]->from = n;
e[1]->from = e[3]->from = n + 1;
e[2]->from = e[4]->from = n + 2;
for (int i = 0; i < 3; i++) {
e[i]->inv = e[i + 3];
e[i + 3]->inv = e[i];
}
face.resize(2);
addFace(e[0], e[1], e[2], 0);
addFace(e[5], e[4], e[3], 1);
for (int i = 0; i < 3; i++)
vertex[i + n] = e[i];
bucket[1].resize(n);
std::iota(begin(bucket[1]), end(bucket[1]), 0);
belong.assign(n, 1);
}
std::vector<Edge *> vertex, face;
std::vector<std::vector<int>> bucket;
std::vector<int> belong;
PS ps;
const int n;
static constexpr int Inf = int(1e8);
Delaunay(const PS &initPs) : n{(int)initPs.size()}, ps(initPs) {
init();
for (int i = 0; i < n; i++) {
addPoint(i);
Edge *e = vertex[i];
for (int j = 0; j < 3; j++) {
if (flip(i, e->r->inv)) {
e = e->l->inv;
j -= 2;
} else {
e = e->inv->r;
}
}
}
}
bool inFace(Point p, int fid) {
int cnt = 0;
Edge *e = face[fid];
do {
auto a = ps[e->from];
e = e->r;
auto b = ps[e->from];
cnt += (b - a) % (p - a) > 0;
} while (e != face[fid]);
return cnt == 3 or cnt == 0;
}
void addPoint(int pid) {
int fid[3] = {belong[pid], face.size(), face.size() + 1};
auto pointS = bucket[fid[0]];
bucket[fid[0]].clear();
face.resize(face.size() + 2);
std::vector<Edge *> e(6);
for (int i = 0; i < 6; i++) {
e[i] = new Edge();
}
for (int i = 0; i < 6; i++) {
e[i]->inv = e[i ^ 1];
}
e[1]->from = e[3]->from = e[5]->from = pid;
Edge *tmpe = face[fid[0]];
int r = 0, l = 5;
for (int j = 0; j < 3; j++) {
Edge *tmpr = tmpe->r;
int b = tmpr->from;
e[r]->from = b;
addFace(e[l], tmpe, e[r], fid[j]);
r = (r + 2) % 6, l = (l + 2) % 6;
tmpe = tmpr;
}
vertex[pid] = e[1];
for (int p : pointS) {
if (p == pid)
continue;
for (int j = 0; j < 3; j++) {
if (inFace(ps[p], fid[j])) {
belong[p] = fid[j];
bucket[fid[j]].push_back(p);
break;
}
}
}
}
bool flip(int pid, Edge *e) {
if (e->face == 0)
return false;
auto fir = e->inv->l;
int inCircleRes = inCircle(ps[pid], ps[fir->r->from],
ps[fir->l->from], ps[e->l->from]);
if (inCircleRes >= 0)
return false;
int fid[2] = {fir->face, e->face};
auto pointS = bucket[fid[0]];
pointS.insert(pointS.end(), bucket[fid[1]].begin(), bucket[fid[1]].end());
bucket[fid[0]].clear();
bucket[fid[1]].clear();
auto ev = e->inv;
auto sec = e->r, thir = e->l, four = fir->l;
addFace(fir, sec, ev, fid[0]);
addFace(e, thir, four, fid[1]);
e->from = pid;
ev->from = thir->from;
for (int p : pointS) {
for (int j = 0; j < 2; j++) {
if (inFace(ps[p], fid[j])) {
belong[p] = fid[j];
bucket[fid[j]].push_back(p);
break;
}
}
}
return true;
}
};
点（三维）
Point (3D)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137template <class T, class G>
struct BaseVector3 {
T x, y, z;
constexpr BaseVector3() : BaseVector3(T{}, T{}, T{}) {}
constexpr BaseVector3(T x, T y, T z)
: x{x}, y{y}, z{z} {}
constexpr BaseVector3 operator-(BaseVector3 a) const {
return BaseVector3(x - a.x, y - a.y, z - a.z);
}
constexpr BaseVector3 operator-() const {
return BaseVector3(-x, -y, -z);
}
constexpr BaseVector3 operator+(BaseVector3 a) const {
return BaseVector3(x + a.x, y + a.y, z + a.z);
}
constexpr G operator*(BaseVector3 a) const {
return x * a.x + y * a.y + z * a.z;
}
constexpr BaseVector3 operator%(BaseVector3 a) const {
return BaseVector3(
y * a.z - a.y * z,
a.x * z - x * a.z,
x * a.y - a.x * y);
}
constexpr friend BaseVector3 operator*(T d, BaseVector3 a) {
return BaseVector3(d * a.x, d * a.y, d * a.z);
}
constexpr friend bool sameLine(BaseVector3 a, BaseVector3 b) {
return dis2(a % b) == 0;
}
constexpr friend bool sameDir(BaseVector3 a, BaseVector3 b) {
return samLine(a, b) and a * b >= 0;
}
// 字典序
constexpr bool operator<(BaseVector3 a) const {
if (x != a.x)
return x < a.x;
if (y != a.y)
return y < a.y;
return z < a.z;
}
constexpr bool operator==(BaseVector3 a) const {
return x == a.x and y == a.y and z == a.z;
}
constexpr friend auto &operator>>(std::istream &is, BaseVector3 &p) {
return is >> p.x >> p.y >> p.z;
}
constexpr friend auto &operator<<(std::ostream &os, BaseVector3 p) {
return os << '(' << p.x << ", " << p.y << ", " << p.z << ')';
}
};
template <class T, class G>
G dis2(BaseVector3<T, G> a, BaseVector3<T, G> b = BaseVector3<T, G>{}) {
auto p = a - b;
return p * p;
}
template <class T, class G>
auto dis(BaseVector3<T, G> a, BaseVector3<T, G> b = BaseVector3<T, G>{}) {
return sqrtl(dis2(a, b));
}
template <class T, class G>
auto area(BaseVector3<T, G> a, BaseVector3<T, G> b = BaseVector3<T, G>{}) {
return dis(a % b) / 2;
}
template <class T>
struct TrianglePatch {
std::array<T, 3> vertexs;
constexpr TrianglePatch() : vertexs{} {}
constexpr TrianglePatch(T u, T v, T w)
: vertexs({u, v, w}) {}
constexpr T &operator[](int i) {
return vertexs[i];
}
constexpr T normal() const {
return (vertexs[1] - vertexs[0]) % (vertexs[2] - vertexs[0]);
}
constexpr T vectorTo(T a) const {
return a - vertexs[0];
}
constexpr auto area() const {
return ::area(vertexs[1] - vertexs[0], vertexs[2] - vertexs[0]);
}
constexpr bool coPlane(T a) const {
return vectorTo(a) * normal() == 0;
}
constexpr bool left(T a) const {
return vector(a) * normal() > 0;
}
constexpr bool contains(T a) const {
if (!coPlane(a)) {
return false;
}
T norm = normal();
int leftCnt = 0;
for (int i = 0; i < 3; i++) {
T edge = vertexs[(i + 1) % 3] - vertexs[i];
T to_a = a - vertexs[i];
leftCnt += sameDir(edge % to_a, norm);
}
return leftCnt == 3;
}
};
using Point = BaseVector3<Float, Float>;
using Vector = Point;
using PS = std::vector<Point>;
using PatchS = std::vector<TrianglePatch<Point>>;
三维凸包
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54PatchS convex(PS ps) {
std::sort(begin(ps), end(ps));
ps.erase(std::unique(ps.begin(), ps.end()), ps.end());
// 去除重复点
const int n = ps.size();
if (n < 4) {
return {};
}
std::vector vis(n, std::vector<int>(n, -1));
using IndexPatch = std::array<int, 3>;
std::vector<IndexPatch> pls(2);
pls[0] = IndexPatch{0, 1, 2};
pls[1] = IndexPatch{0, 2, 1};
auto isAbove = [&](Point p, IndexPatch &pl) {
auto vec = (ps[pl[1]] - ps[pl[0]]) % (ps[pl[2]] - ps[pl[0]]);
return vec * (p - ps[pl[0]]) >= 0;
};
for (int i = 3; i < n; i++) {
std::vector<IndexPatch> res, del;
for (int j = 0; j < size(pls); j++) {
if (!isAbove(ps[i], pls[j])) {
res.push_back(pls[j]);
} else {
del.push_back(pls[j]);
for (int k = 0; k < 3; k++) {
int r = (k + 1) % 3;
vis[pls[j][k]][pls[j][r]] = i;
}
}
}
for (auto pl : del) {
for (int k = 0; k < 3; k++) {
int r = (k + 1) % 3;
if (vis[pl[k]][pl[r]] == i and vis[pl[r]][pl[k]] != i) {
res.push_back({pl[k], pl[r], i});
}
}
}
std::swap(res, pls);
}
PatchS ans;
for (auto pl : pls) {
ans.push_back({ps[pl[0]], ps[pl[1]], ps[pl[2]]});
}
return ans;
}
其他
离散化
Discreter
高精
BINT
快读
FastIO
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29namespace IO{
char ibuf[(1 << 20) + 1], *iS, *iT;
#if ONLINE_JUDGE
#define gh() (iS == iT ? iT = (iS = ibuf) + fread(ibuf, 1, (1 << 20) + 1, stdin), (iS == iT ? EOF : *iS++) : *iS++)
#else
#define gh() getchar()
#endif
#define reg register
inline long long read () {
reg char ch = gh();
reg long long x = 0;
reg char t = 0;
while (ch < '0' || ch > '9') t |= ch == '-', ch = gh();
while (ch >= '0' && ch <= '9') x = x * 10 + (ch ^ 48), ch = gh();
return t ? -x : x;
}
inline void write(long long x) {
if (x < 0) {
x = ~(x - 1);
putchar('-');
}
if (x > 9)
write(x / 10);
putchar(x % 10 + '0');
}
}
//
using IO::read;
using IO::write;
FastI
1
2
3
4
5
6
7
8
9
10
11template<typename T>
void read(T &r) {
r = 0;
static char ch, last;
ch = getchar(), last = 'z';
while (ch < '0' || ch > '9') last = ch, ch = getchar();
while (ch >= '0' && ch <= '9') r = (r << 1) + (r << 3) + (ch ^ 48), ch = getchar();
r = (last == '-') ? -r : r;
}
template<typename T, typename...Ts>
void read(T &arg, Ts&...arg_left) { read(arg); read(arg_left...); }
按popcount状压枚举
Iterator Bitmask With Popcount
最大子矩形
给定方格图，图上有一些障碍点，求最大子矩形，内部不含障碍点
MaxSubRect（O(s^2)）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
i64 MaxSubRect(int n, int m, std::vector<std::pair<int, int>> nod) {//O(s^2)
nod.emplace_back(n, 0);
nod.emplace_back(n, m);
nod.emplace_back(0, m);
nod.emplace_back(0, 0);
i64 ans = 0;
std::sort(nod.begin(), nod.end(), [](const std::pair<int, int>& a, const std::pair<int, int>& b){
if (a.first != b.first) return a.first < b.first;
return a.second < b.second;
});
int s = nod.size();
for (int i = 0; i < s; ++i){
int h1 = m, h2 = 0, k = n - nod[i].first, flag = 0;
for (int j = i + 1; j < s; ++j) {
if (nod[j].second <= h1 && nod[j].second >= h2) {
if (k * (h1 - h2) <= ans) break;//剪枝：如果走到边界的距离乘高都比现有答案小，break
ans = std::max(ans, 1ll * (h1 - h2) * (nod[j].first - nod[i].first));
if (nod[i].second == nod[j].second) {//如果高度相同，可以直接break且不用考虑边界
flag = 1;
break;
}
if (nod[j].second > nod[i].second)
h1 = std::min(h1, nod[j].second);
else
h2 = std::max(h2, nod[j].second);
}
}
if (!flag) ans = std::max(ans, 1ll * k * (h1 - h2));//枚举障碍点,默认向右只能到达最右边的障碍点，而不是右边界，所以应该考虑直接往右边界走的情况
h1 = m, h2 = 0, k = nod[i].first, flag = 0;
for (int j = i - 1; j >= 0; --j) {//往左走，类似
if (nod[j].second <= h1 && nod[j].second >= h2) {
if (k * (h1 - h2) <= ans) break;
ans = std::max(ans, 1ll * (h1 - h2) * (nod[i].first - nod[j].first));
if (nod[i].second == nod[j].second) {
flag = 1;
break;
}
if (nod[j].second > nod[i].second)
h1 = std::min(h1, nod[j].second);
else
h2 = std::max(h2, nod[j].second);
}
}
if (!flag) ans = std::max(ans, 1ll * k * (h1 - h2));
}
std::sort(nod.begin(), nod.end(), [](std::pair<int, int> a, std::pair<int, int> b) {
if (a.second != b.second) return a.second < b.second;
return a.first < b.first;
}); //考虑两边都是边界
for (int i = 0; i < s - 1; ++i)
ans = std::max(ans, 1ll * n * (nod[i + 1].second - nod[i].second));
return ans;
}
MaxSubRect（O(nm)）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30i64 MaxSubRect(std::vector<std::vector<bool>> &mmap) {//O(nm)
int n = mmap.size() - 1, m = mmap[0].size() - 1;
std::vector<std::vector<int>> h(n + 1, std::vector<int>(m + 1)), l = h, r = h;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
h[i][j] = 1;
if (i > 1 && !mmap[i - 1][j] & !mmap[i][j])
h[i][j] = h[i - 1][j] + 1;
l[i][j] = j;
r[i][j] = j;
}
for (int j = 1; j <= m - 1; ++j)
if (!mmap[i][j] & !mmap[i][j + 1])
l[i][j + 1] = l[i][j];
for (int j = m - 1; j >= 1; --j)
if (!mmap[i][j] & !mmap[i][j + 1])
r[i][j] = r[i][j + 1];
}
i64 ans = 0;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j) {
if (i > 1 && !mmap[i - 1][j] & !mmap[i][j]) {
l[i][j] = std::max(l[i - 1][j], l[i][j]);
r[i][j] = std::min(r[i - 1][j], r[i][j]);
}
if (!mmap[i][j])
ans = std::max(ans, 1ll * (r[i][j] - l[i][j] + 1) * h[i][j]);
}
return ans;
}
优先队列维护前k大的数
这里封成struct了，当然，你直接用主要逻辑也行，不封装也行。
template<typename T> struct BUCKET{
int k;
priority_queue<T,vector<T>,greater<T>> q;//前k大（改成less即为前k小）
BUCKET(int k_){k=k_;}
void push(T x){
if(q.size()>=k){
if(q.top()<x){q.pop();q.push(x);}//前k大（改成>即为前k小）
}else q.push(x);
}
vector<T> get(){
vector<T> out;
while(!q.empty()){out.push_back(q.top());q.pop();}
reverse(out.begin(),out.end());
return out;
}
};
//使用方法：
BUCKET<int> buk(k);//创建一个大小为k的桶（我也不知道算不算桶，把它理解成那种往里面加东西，加到桶的容量上限时会溢出来的效果就行）
buk.push(x);//往桶里装东西
auto vec=buk.get();//把桶里的东西倒出来
//特别注意，如果你要用封装的话，T的类型要保证支持
//operator<(T a,T b)
//operator>(T a,T b)
//operator<(const T a,T b)
//operator>(const T a,T b)
//不然会报错
min25筛
一种能在亚线性时间复杂度内求积性函数前缀和的算法。
使用条件：
- 求和函数具有积性 $f(ab) = f(a)f(b)$
- $f(1) = 1$
- $f(p^k)$ 能够被快速计算
例如： 积性函数 $f(p^k) = p^k (p^k - 1)$ 可以拆成两个积性函数 $x^2$ 和 $-x$ 的和。而且 $p^k$ 确实很容易求出（式子已经给出）。那么拆成一个两项的多项式f，然后分别求前缀和pref，最后合并贡献即可。
有些函数可能不完全符合上述条件，但是你可以选择分类讨论解决之
幂数 求和公式 $1$ $n$ $x$ $\frac{n(n + 1)}{2}$ $x^2$ $\frac{n(n + 1)(2n + 1)}{6}$ $x^3$ $[\frac{n(n + 1)}{2}]^2$ $\dots$ $\dots$ $x^k$ $\frac{1}{k + 1}[(n + 1)^{k + 1} - 1 - \sum_{i = 0}^{k - 1}C_{k + 1}^i(\sum_{m = 1}^{n}m^i)]$
MIN25
神秘结论
$O(1)$ 求 $1$ 到 $n$ 的前缀异或和
PreXorSum
前面的区域以后再来探索吧！